Discussion Overview
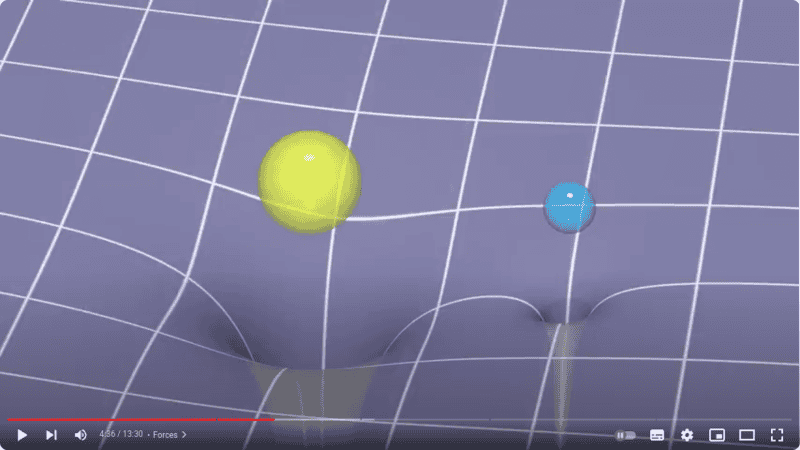
The discussion revolves around the feasibility of creating a working model to demonstrate the Lagrange points L4 and L5 using a rotating surface. Participants explore both theoretical and practical aspects of this concept, including potential challenges and implications.
Discussion Character
- Exploratory, Technical explanation, Debate/contested
Main Points Raised
- One participant proposes fabricating a surface that rotates around a vertical axis to allow a bead to roll in an orbit around L4 or L5, questioning its feasibility in principle and the practical challenges involved.
- Another participant references existing models based on Newtonian mechanics, suggesting that there are already effective demonstrations of similar concepts.
- A participant expresses difficulty accessing a referenced site, indicating a potential barrier to further exploration of the topic.
- One participant believes that while the concept could work in principle, practical challenges such as high friction, vibration from the turntable, and the precision required in manufacturing the gravity well shape could hinder success.
- Another participant shares a video of a similar concept that appears to work well but notes that the complexity of the L4-L5 problem introduces additional challenges. They also mention the potential impact of gyroscopic effects on the behavior of the rolling bead, suggesting it could either complicate or enhance the model's functionality.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the feasibility of the model; while some believe it could work in principle, others highlight significant practical challenges that may prevent successful implementation.
Contextual Notes
Participants mention various practical limitations, such as the need for precise manufacturing of the surface and control over the turntable speed, which remain unresolved in the discussion.
