- #1
MrNerd
- 81
- 0
I'm sure someone has already thought of this somewhere, but can a wormhole violate the conservation of energy IF the object takes two paths?
I mean like this:
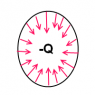
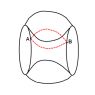
Imagine a wormhole near a charged object, one closer, the other farther. Then imagine the particle being attracted to the charged object(Path 1) It has now lost potential energy. BUT then it goes back away through the wormhole, a shortcut in space(Path 2). The object travels the full distance relative to an outside observer. The object travels a shrunken distance relative to itself(Doesn't it?) Would it not take less energy through the wormhole to gain back the initial potential energy? This is also not relying on gravitational acceleration, which is technically nonexistent and only curves paths. The only thing I can reasonably think of is that either wormholes are impossible, thus negating this paradox entirely, or the field is kind of 'condensed' into the wormhole passage thingie.
On an unrelated note, how has no one ever thought of an explanation in science fiction for being able to communicate with extremely distant ships and bases? The whole point of the warp drive or whatever is to get them to places that are further than light can reach in traversable time. Since em waves travel at light speed, they should probably die before the messages even reach them(depending on distance). Unless they have a permanent wormhole for the communications, or they generate one everytime they send a message and just send a communications probe thing through, this just seems completely, even in science fiction reasoning, unreasonable.
I mean like this:
Imagine a wormhole near a charged object, one closer, the other farther. Then imagine the particle being attracted to the charged object(Path 1) It has now lost potential energy. BUT then it goes back away through the wormhole, a shortcut in space(Path 2). The object travels the full distance relative to an outside observer. The object travels a shrunken distance relative to itself(Doesn't it?) Would it not take less energy through the wormhole to gain back the initial potential energy? This is also not relying on gravitational acceleration, which is technically nonexistent and only curves paths. The only thing I can reasonably think of is that either wormholes are impossible, thus negating this paradox entirely, or the field is kind of 'condensed' into the wormhole passage thingie.
On an unrelated note, how has no one ever thought of an explanation in science fiction for being able to communicate with extremely distant ships and bases? The whole point of the warp drive or whatever is to get them to places that are further than light can reach in traversable time. Since em waves travel at light speed, they should probably die before the messages even reach them(depending on distance). Unless they have a permanent wormhole for the communications, or they generate one everytime they send a message and just send a communications probe thing through, this just seems completely, even in science fiction reasoning, unreasonable.