H2instinct
- 20
- 0
Complex Numbers Proof
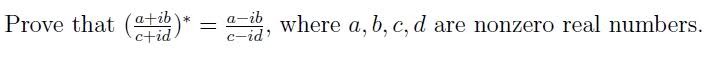
Multiplying the top and bottom by the complex conj. of the bottom:
\frac{a+ib}{c+id} * \frac{c-id}{c-id}
Gives me:
\frac{(ac+bd) - i(ad-bc)}{c^{2}+d^{2}}
In form x+iy it is:
\frac{(ac+bd)}{c^{2}+d^{2}} + (\frac{(bc-ad)}{c^{2}+d^{2}})*i
This is where I get stuck. In order to prove \left(\frac{a+ib}{c+id}\right)*\equiv\frac{a-ib}{c-id} I think that I am supposed to take the complex conjugate of my previous answer and then work backwards until I get to \frac{a-ib}{c-id}. I have tried this with several different variations and I am not coming up with the proof at all. I need a bump in the right direction here.
Multiplying the top and bottom by the complex conj. of the bottom:
\frac{a+ib}{c+id} * \frac{c-id}{c-id}
Gives me:
\frac{(ac+bd) - i(ad-bc)}{c^{2}+d^{2}}
In form x+iy it is:
\frac{(ac+bd)}{c^{2}+d^{2}} + (\frac{(bc-ad)}{c^{2}+d^{2}})*i
This is where I get stuck. In order to prove \left(\frac{a+ib}{c+id}\right)*\equiv\frac{a-ib}{c-id} I think that I am supposed to take the complex conjugate of my previous answer and then work backwards until I get to \frac{a-ib}{c-id}. I have tried this with several different variations and I am not coming up with the proof at all. I need a bump in the right direction here.
Last edited: