What is the instantaneous value of UL after commutation?

[builder_user]

Homework Statement

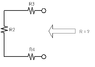
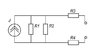
Find instantaneous value UL after commutation.

Homework Equations

type of commutation - switch key(I hope I've translated it correct)
Use operator method and classic method

The Attempt at a Solution

K1=1.2
K2=0.7
K3=1
J=8*K1
L=10*K1
R1=K2*8
R2=K2*8
R3=4*K3
R4=12*K3

I need to find UL in the moment of commutation?

 

[Quinzio]

I need to find UL in the moment of commutation?

It looks like that.
Even if it wasn't, find it.

 

[builder_user]

Before commutation R1=0?

What to do with J?

 

[Quinzio]

Does current flow in R1 before commutation ? After ?

J is J... it's a current generator and it does its job.

 

[builder_user]

Does current flow in R1 before commutation ? After ?

I don't know.

I think before commutation all currents and voltage was 0.

But what is the main algorithm at all for this task for classic method?

 

[gneill]

Is it only the voltage across the inductor immediately after commutation of the switch that is required? Not the voltage as a function of time?

I don't know exactly what is meant by "classical method" versus "operator method", unless the first wants a 'down and dirty' differential equation approach and the latter a Laplace transform approach or something along those lines.

Personally, I'd just recognize that the circuit is going to transition between two states, the first being the steady state before the switch is thrown, and the second the steady state that will eventually hold a long time after the switch is thrown. Throwing the switch will be like hitting the circuit with a step function in terms of change of current. The circuit has only L and R components, so it'll have a time constant.

It might be instructive to derive the Norton equivalents for the before and after states and see what the difference really is.

Things to keep in mind: Inductors "don't like" sudden changes in current, they'll happily react with any voltage they have to in order to try to maintain the status quo (at least very briefly!); So, constant current through the inductor over the instant of commutation. Also, when drawing up the post-switching event equivalent circuit, it's fair game to put a current source in series with the inductor that drives the same current as the inductor carried prior to the switch being thrown. This has the effect of carrying the previous state of the circuit along as the initial condition for the new one. That current has to go somewhere... and it won't be through the main current supply!

 

[builder_user]

Is it only the voltage across the inductor immediately after commutation of the switch that is required? Not the voltage as a function of time?

I only have translated the task. I think the result need to be like this
u(t)=U0*(1*e^(t/T))

I don't know exactly what is meant by "classical method" versus "operator method", unless the first wants a 'down and dirty' differential equation approach and the latter a Laplace transform approach or something along those lines.

Yes

 

[builder_user]

The main problem is
how to calculate circuit in every case(after,before,in the moment of commutation)

 

[gneill]

The main problem is
how to calculate circuit in every case(after,before,in the moment of commutation)

You should be able to use what you know about the properties of inductors in DC circuits to determine the steady state conditions that will hold before switching and a "long time" after. Have you done that?

 

[builder_user]

Before comutation - L1 does not exist in the circuit 'cause there is not U?
After commutation UL exists right?

After commutation
U(t)=(Ur3+Ul(t)+Ur4)
because Ur2=Ur1=Ur3+UL(t)+Ur4?

 

[gneill]

Before comutation - L1 does not exist in the circuit 'cause there is not U?
After commutation UL exists right?

After commutation
U(t)=(Ur3+Ul(t)+Ur4)
because Ur2=Ur1=Ur3+UL(t)+Ur4?

When you say, "L1 does not exist in the circuit", you need to be a bit careful. At steady state in a DC powered circuit the voltage across an inductor will be zero, but it will be carrying current and storing energy in its magnetic field, so that when some change occurs to alter the circuit conditions that energy is available to generate counteracting voltages.

So just before the switch is closed UL will be zero and the current through the inductor will be, say, IL. When the switch is closed, the circuit will be driven towards a new steady state where IL will be different. The inductor wants to keep its current flowing at the IL rate, and "resists" the change of state by producing a voltage to try to keep it so.

Have you drawn the Norton equivalent circuits of the networks feeding the inductor for both steady states?

 

[builder_user]

Have you drawn the Norton equivalent circuits of the networks feeding the inductor for both steady states?

But before commutation I have only resistors and current source. I can only find the resitance of circuit.

 

[gneill]

But before commutation I have only resistors and current source. I can only find the resitance of circuit.

Exactly. Replace the whole resistor network and its current source with a single resistor and current source. Do it for the before- and after-switching steady states. You want to reduce it to the form shown in the attached figure.

 

[builder_user]

Will resistor R1 exist after commutation?

 

[gneill]

Will resistor R1 exist after commutation?

Yes, when the switch is closed R1 will be in parallel with R2.

 

[builder_user]

Yes, when the switch is closed R1 will be in parallel with R2.

And it will exist and in the state of rest too?

 

[gneill]

And it will exist and in the state of rest too?

Yes, but of course with the inductor paralleling it, at steady state it will draw no current since all the current will be passing through the inductor.

Don't worry too much about the details of the end states yet. Get the Norton equivalents drawn and then we'll examine the results.

 

[builder_user]

Is it wrong?

 

[gneill]

Perhaps you're not familiar with Norton equivalents? Both before and after circuits should look just as I showed in post #13. Of course, the values for the resistor and the current source will differ for the two cases.

To find the Norton equivalent, temporarily remove the inductor from the circuit and also remove the current source. That will leave you with just the resistor network. Find the equivalent resistance of the resistor network looking into where the inductor was connected. Next, replace the current source and place a short circuit across where the inductor was connected. Find the current passing through that shorting wire.
Assign the resistance you found to RN in the equivalent circuit, and the current value you found to the new current supply of that equivalent.

 

[builder_user]

Perhaps you're not familiar with Norton equivalents?

Yes.I've never heard about it.Maybe in Russian it has another name.(Like Thevenin equivalent for example)

To find the Norton equivalent, temporarily remove the inductor from the circuit and also remove the current source. That will leave you with just the resistor network. Find the equivalent resistance of the resistor network

(R1*R3+R4*R1+R2*R1+R2*R3+R2*R4)/(R1*R2*(R3+R4)?

looking into where the inductor was connected. Next, replace the current source and place a short circuit across where the inductor was connected.

I don't understand.

Assign the resistance you found to RN in the equivalent circuit, and the current value you found to the new current supply of that equivalent.

When did I find it?I only have resistance of all circuit.

 

[gneill]

Are you familiar with Thevenin equivalents then?

 

[builder_user]

Are you familiar with Thevenin equivalents then?

Yes,I am.(I think so).It was the first task in my work.

 

[gneill]

Yes,I am.(I think so).It was the first task in my work.

Excellent. Norton equivalents are just like Thevenin equivalents, only the source is a current rather than a voltage.

Proceed in the same way you would to find the Thevenin equivalent resistance. The Norton resistance is exactly the same.

To find the Thevenin voltage the procedure is to find the open-circuit voltage at the terminals. For the Norton current, you place a short circuit across the terminals and find the current running through it.

Alternatively, you can find the Thevenin equivalent model, and then the Norton current is given by the Thevenin voltage divided by the Thevenin resistance (as you can see, the Thevenin and Norton equivalents are closely related!).

 

[builder_user]

But when I want to find Thevenin equivalents I have this(pic.) thing where I want to find U.
But in my circut I do not have potential difference(?).I think I have to make some algorithm to make it more understandable.

 

[gneill]

For the case before the switch is closed, you have the following circuit (minus the inductance) for which you want to find the Thevenin (and then the Norton) equivalent circuits. Can you find the open-circuit voltage for this network?

 

[builder_user]

For the case before the switch is closed, you have the following circuit (minus the inductance) for which you want to find the Thevenin (and then the Norton) equivalent circuits. Can you find the open-circuit voltage for this network?

I do not have enough equatations.even when I replace J with E I'll not have current.
One circuit but one equatation.

 

[gneill]

Is it R3 and R4 that are confusing the issue? When the inductor is removed and the circuit is open as I showed, they are not part of complete circuits. So no current will flow though them. That also means that no voltage drop will occur across them. So the output voltage is the same as the voltage drop across R2.

 

[builder_user]

is it r3 and r4 that are confusing the issue? When the inductor is removed and the circuit is open as i showed, they are not part of complete circuits. So no current will flow though them. That also means that no voltage drop will occur across them. So the output voltage is the same as the voltage drop across r2.

u=j*r2?

 

[gneill]

u=j*r2?

Yes. That will be the Thevenin voltage. What did you get for the Thevenin resistance?

 

[builder_user]

Yes. That will be the Thevenin voltage. What did you get for the Thevenin resistance?

Don't understand the question.
R for resistors' circuit?

 

[gneill]

A Thevenin equivalent circuit consists of a voltage source (the Thevenin Voltage) and a resistance (the Thevenin Resistance). What are they for the circuit in question?

 

[builder_user]

A Thevenin equivalent circuit consists of a voltage source (the Thevenin Voltage) and a resistance (the Thevenin Resistance). What are they for the circuit in question?

Rth=(R1*R3+R4*R1+R2*R1+R2*R3+R2*R4)/(R1*R2*(R3+R4)) or Rth=R2.I'm not sure.

 

[gneill]

To find the Thevenin resistance you suppress the sources (Remove them by shorting voltage sources and removing current sources) and then find the equivalent resistance of what's left. What's the equivalent resistance in the attached figure?

 

[builder_user]

Oh.R=R2+R3+R4
I found for all curcit...But not for this.

This results for state "before commutation",right?

 

[gneill]

Okay! So you have the Thevenin equivalent for the network that's driving the inductor. To put numbers to them, R_TH = 21.6 and V_TH = 53.76. Correct?

Now, the Norton equivalent circuit has the same resistor value as the Thevenin equivalent, and the voltage source is replaced with a current source of V_TH/R_TH. The resistor is in parallel with the current source.

Do the same work for the case after the switch is closed. Note that all the switch does is put R1 in parallel with R2. What numbers do you get for the Norton equivalent in this case?

 

[builder_user]

Do the same work for the case after the switch is closed. Note that all the switch does is put R1 in parallel with R2. What numbers do you get for the Norton equivalent in this case?

But when switch is closed there is the inductive element.It resistance add too?




This circuit after commutation?

 

[gneill]

But when switch is closed there is the inductive element.His resistance add too?

We're treating the inductor as the load being driven by a Norton equivalent of the source network. It plays no part in finding the equivalent circuit for the source network.

So no, there is no inductor added to the source network by the switch. It only adds R1 in parallel with R2 to the circuit we just analyzed. We will deal with the inductor after we have the equivalent circuits for the sources.

What we want to end up with is two Norton equivalent circuits, one for each state of the switch. These two equivalent circuits replace the current source and resistor networks of the original circuit. These equivalent circuits will be "driving" the inductor. They will make it easy to analyze what happens when the switch is closed.

 

[builder_user]

We're treating the inductor as the load being driven by a Norton equivalent of the source network. It plays no part in finding the equivalent circuit for the source network.

So no, there is no inductor added to the source network by the switch. It only adds R1 in parallel with R2 to the circuit we just analyzed. We will deal with the inductor after we have the equivalent circuits for the sources.

What we want to end up with is two Norton equivalent circuits, one for each state of the switch. These two equivalent circuits replace the current source and resistor networks of the original circuit. These equivalent circuits will be "driving" the inductor. They will make it easy to analyze what happens when the switch is closed.

After replacing there will be diff. equatations?
So this scheme?
and
R=R1*R2/(R1+R2)
U=J*R

 

[gneill]

I'll show you how to analyze the circuit without differential equations to begin with. That way you'll know what result you're looking for!

Yes, the figure you provided is the circuit of the source network after commutation of the switch. You want to find its Norton equivalent, just like you did for when the switch was open. What's its Norton resistance and current?

 

[builder_user]

I'll show you how to analyze the circuit without differential equations to begin with. That way you'll know what result you're looking for!

But I must find U as time function...like this
U=900/375*e^375t+C


The problem is...I must use differential equatations.But they only need at the moment of commutation.With Laplace and without it(especially for LC).It's the task.

 

[builder_user]

What's its Norton resistance and current?

Strange but currents are the same.

 

[gneill]

But I must find U as time function...like this
U=900/375*e^375t+C


The problem is...I must use differential equatations.But they only need at the moment of commutation.With Laplace and without it(especially for LC).It's the task.

The equivalent circuits will allow you to write the differential equations very easily. In fact, you will probably already have done so for circuits in this basic form!

I will show you how to write the desired U(t) function by inspection, so that you can check your differential equation result. Will that work for you?

 

[gneill]

Strange but currents are the same.

I think you may have forgotten about R3 and R4...

 

[builder_user]

I think you may have forgotten about R3 and R4...

I found U.
U/R3=J3
U/R4=J4?

 

[builder_user]

The equivalent circuits will allow you to write the differential equations very easily. In fact, you will probably already have done so for circuits in this basic form!

I will show you how to write the desired U(t) function by inspection, so that you can check your differential equation result. Will that work for you?

I need equations like this

from example
moment of commutation
UL=Ldi/dt

i2+i3=i1
i1*R1+i2*R3=E
-i2*R3+i3*R4+Ldi3/Dt=0

-E-i3*R1/(R1+R3)*R3+i3*R4+Ldi3/dt=0
i3=2.4+c*e^-375t

i(0)=1.7(before commut.)
2.4+c*e^0=1.7
c=-0.7

i3(t)=2.4-0.7*e^-375t

 

[gneill]

I found U.
U/R3=J3
U/R4=J4?

What are J3 and J4?

If you are looking at the Thevenin equivalent of your circuit, there is no current through R3 or R4. The Thevenin voltage is produced by the current flowing through the parallel combination of R1 and R2. The Thevenin resistance is the sum of R3 and R4 and the parallel combination of R1 and R2.

The Norton resistance, R_N, is the same as the Thevenin resistance. The Norton current is V_TH/R_TH.

 

[builder_user]

I see.Operator method it seems to similar
find i before and after commutation
replace inductor with operator resistor
p=j*w - operator.

 

[gneill]

I need equations like this

from example
moment of commutation
UL=Ldi/dt

i2+i3=i1
i1*R1+i2*R3=E
-i2*R3+i3*R4+Ldi3/Dt=0

-E-i3*R1/(R1+R3)*R3+i3*R4+Ldi3/dt=0
i3=2.4+c*e^-375t

i(0)=1.7(before commut.)
2.4+c*e^0=1.7
c=-0.7

i3(t)=2.4-0.7*e^-375t

The equations will be easy to write from the equivalent circuits. You will have only to deal with one current source, one resistor, and one inductor. Your textbook probably has this form as an example!

 

[builder_user]

The equations will be easy to write from the equivalent circuits. You will have only to deal with one current source, one resistor, and one inductor. Your textbook probably has this form as an example!

so, for L i'll just need to use U=Ldi/dt?

 

[gneill]

I see.


Operator method it seems to similar
find i before and after commutation
replace inductor with operator resistor
p=j*w - operator.

Yes. Certainly.

What I've been trying to do is reduce the before and after commutation circuits to their very simplest forms so that it will be very easy to apply any method of circuit analysis you wish to use. They will be so basic that your textbook should already provide a solved example.