2milehi
- 146
- 20
So I ran across this problem on the 'net and I can't determine "x". The arc length of the circle is 360.
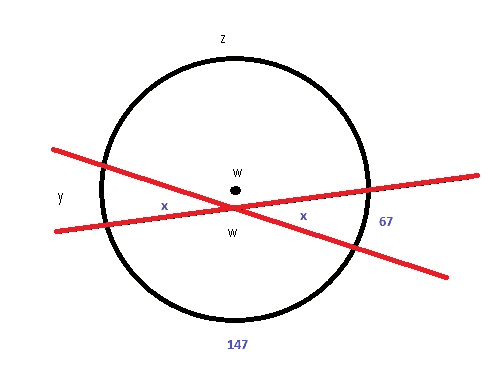
I added some other variable and took what I know about a circle and intersecting lines. I wound up with four variables and four equations.
x = 1/2 (y + 67)
w = 1/2 (z + 147)
y + z + 67 + 147 = 360
2w + 2x = 360
and into matrix form
1w + 1x + 0y + 0z = 180
0w + 1x - 1/2y + 0z = 67/2
1w + 0x - 0y - 1/2z = 147/2
0w + 0x + 1y + 1z = 146
But that comes up with an indeterminate.
Taking a closer look before I post, I see that three of the equations relate to length and one relates to degrees. But with s = r · theta, r is such that s = theta in degrees.
I am stuck now
I added some other variable and took what I know about a circle and intersecting lines. I wound up with four variables and four equations.
x = 1/2 (y + 67)
w = 1/2 (z + 147)
y + z + 67 + 147 = 360
2w + 2x = 360
and into matrix form
1w + 1x + 0y + 0z = 180
0w + 1x - 1/2y + 0z = 67/2
1w + 0x - 0y - 1/2z = 147/2
0w + 0x + 1y + 1z = 146
But that comes up with an indeterminate.
Taking a closer look before I post, I see that three of the equations relate to length and one relates to degrees. But with s = r · theta, r is such that s = theta in degrees.
I am stuck now