- #1
jbar18
- 53
- 0
Hi,
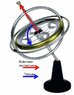
I'm having some trouble understanding how this works. I'm trying to put the pieces together but I'm hoping people here can help me. Specifically I'm wondering about a gyroscope positioned so that its axis lies in the horizontal plane and one end sits on top of a rod. So far what I've got is this:
There is a torque acting at the centre of mass of the gyroscope. Torque equals the rate of change of angular momentum, and so the angular momentum of the gyroscope must change so long as there is a torque acting.
Angular momentum must be conserved. I'm not really sure how that applies here. Maybe this is why I'm having trouble.
The main problem I'm having is this: It sounds logical when somebody else says it, but I can't seem to properly understand it myself. If this works on a gyroscope, why doesn't it work on a stationary rod (this still has a torque acting?). In this case the rod would gain angular momentum in the vertical plane I guess, due to gravity. So then if the rod is spun, like a gyroscope, it should precess as well? Maybe it does a little bit, but no matter how thick or heavy or long the rod is, it will always fall pretty quick. So why is this different for a gyroscope?
I've been thinking and thinking but I just can't really clear it up. Any help appreciated. Thanks.
I'm having some trouble understanding how this works. I'm trying to put the pieces together but I'm hoping people here can help me. Specifically I'm wondering about a gyroscope positioned so that its axis lies in the horizontal plane and one end sits on top of a rod. So far what I've got is this:
There is a torque acting at the centre of mass of the gyroscope. Torque equals the rate of change of angular momentum, and so the angular momentum of the gyroscope must change so long as there is a torque acting.
Angular momentum must be conserved. I'm not really sure how that applies here. Maybe this is why I'm having trouble.
The main problem I'm having is this: It sounds logical when somebody else says it, but I can't seem to properly understand it myself. If this works on a gyroscope, why doesn't it work on a stationary rod (this still has a torque acting?). In this case the rod would gain angular momentum in the vertical plane I guess, due to gravity. So then if the rod is spun, like a gyroscope, it should precess as well? Maybe it does a little bit, but no matter how thick or heavy or long the rod is, it will always fall pretty quick. So why is this different for a gyroscope?
I've been thinking and thinking but I just can't really clear it up. Any help appreciated. Thanks.