motoxYogi
- 11
- 0
Hello all,
I am currently doing a design project on gyroscopes.
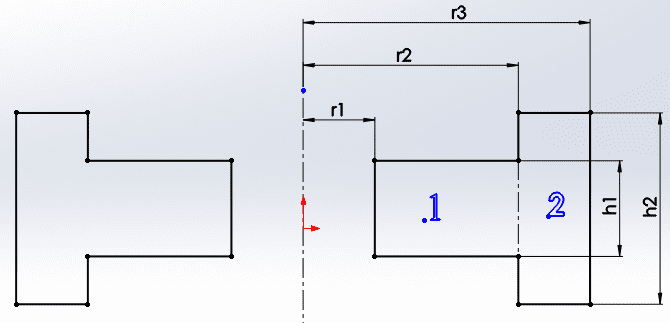
My question concerns the flywheel design, specifically trying to determine the dimensions of a flanged free-spinning flywheel to maximize the moment of inertia while trying to minimize the mass, given certain design constraints.
I've treated the flanged flywheel as two separate hollow cylinders and as far as I understand it, the moment of inertia about the axis of rotation is
I=1/2[m1(r12+r22)+m2(r22+r32)]
The mass is
M=πρ[h1(r22-r12)+h2(r32-r22)]
Due to design constraints r3=0.05m and h2 has a maximum size of 0.04m, due to the bearing I will be using r1 = 0.011 m and h1=0.007m. So the only variable is r2.
The material that i have been using is brass, ρ=8400kg/m3
I know I should be able to use calculus to solve it but I've never been able to apply it well, I've been chasing myself round in circles for days and just keep drawing blanks.
Any help or suggestions is greatly appreciated.
I am currently doing a design project on gyroscopes.
My question concerns the flywheel design, specifically trying to determine the dimensions of a flanged free-spinning flywheel to maximize the moment of inertia while trying to minimize the mass, given certain design constraints.
I've treated the flanged flywheel as two separate hollow cylinders and as far as I understand it, the moment of inertia about the axis of rotation is
I=1/2[m1(r12+r22)+m2(r22+r32)]
The mass is
M=πρ[h1(r22-r12)+h2(r32-r22)]
Due to design constraints r3=0.05m and h2 has a maximum size of 0.04m, due to the bearing I will be using r1 = 0.011 m and h1=0.007m. So the only variable is r2.
The material that i have been using is brass, ρ=8400kg/m3
I know I should be able to use calculus to solve it but I've never been able to apply it well, I've been chasing myself round in circles for days and just keep drawing blanks.
Any help or suggestions is greatly appreciated.