- #1
simpComp
- 44
- 0
Hello,
I am really not very good with math... over the years, I totally lost it. But today, it caught up with me... LOL! I hope someone can help me.
In my spare time I am fiddling around with proximity sensors. I have a proximity sensor that accepts 135 steps. Therefore, when I am at step 135, the sensor is able to detect an object 0 inches away. When I am down at step 0, the sensor is able to detect an object at 135" away which is the maximum distance. So as you can see the higher the steps, the shorter the distance an object can be detected by the sensor.The lower the steps the further the object can be detected by the sensor. The problem is that the relation is not linear, its exponential?
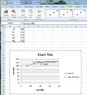
Therefore I need to make a relation between the number of steps and inches. Please view attachment for an example of the curve set by the steps vs the distance!
Here are some definite coordinates that I measured:
(0, 120)
(10,75)
(35,40)
(70,15)
My question is, how can I develop a mathematical model (formula) so that just by looking at a step value I would be able to calculate the respective distance without looking at the
graph?
Thank you all for your help.
I am really not very good with math... over the years, I totally lost it. But today, it caught up with me... LOL! I hope someone can help me.
In my spare time I am fiddling around with proximity sensors. I have a proximity sensor that accepts 135 steps. Therefore, when I am at step 135, the sensor is able to detect an object 0 inches away. When I am down at step 0, the sensor is able to detect an object at 135" away which is the maximum distance. So as you can see the higher the steps, the shorter the distance an object can be detected by the sensor.The lower the steps the further the object can be detected by the sensor. The problem is that the relation is not linear, its exponential?
Therefore I need to make a relation between the number of steps and inches. Please view attachment for an example of the curve set by the steps vs the distance!
Here are some definite coordinates that I measured:
(0, 120)
(10,75)
(35,40)
(70,15)
My question is, how can I develop a mathematical model (formula) so that just by looking at a step value I would be able to calculate the respective distance without looking at the
graph?
Thank you all for your help.
Attachments
Last edited: