- #1
jaumzaum
- 434
- 33
I'm studying special relativity and I'm having difficulty in understanding somethings. I have 2 questions I'm confused about.
1) If I am moving in relation to you, when you observe me, I should be in slow-motion. but you are moving in relation to me, so when I observe you, will you be in slow motion too?
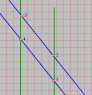
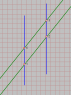
2) Consider the following experiment. Pam and Jim are moving in a 1-dimensional space frame. Pam moves to the right with velocity v (in relation to me, I'm at rest at the origin), and Jim moves to the left with velocity v too. Both are hanging a 1 meter rule in the hands, pointing forward. They have always the same distance in relation to the origin.
Consider the following events
Event 1: the front of the Pam's rule touches Jim
Event 2: the back of the Pam's rule passes Jim
Event 3: the front of the Jim's rule touches Pam
Event 4: the back of the Jim's rule passes Pam
Δt(x,y) = time interval between event x and y measured by Pam
Δt'(x,y) = time interval between event x and y measured by Jim
Δt''(x,y) = time interval between event x and y measured by me
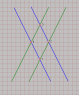
For me, events 1 and 3, 2 and 4 should be simultaneous. But let's analyze Jim's frame of reference. For Jim, event 1 and 2 occur at the same place, so, Jim measures the proper time. Thereby Δt(1,2) > Δt'(1,2)
Also, Δt'(3,4) > Δt(3,4)
For symmetry, Δt(3,4)=Δt'(1,2), Δt(1,2)=Δt'(3,4)
So Δt(1,2)>Δt(3,4)
and the events should not be simultaneous to Jim, the same for Pam
Is this right?
1) If I am moving in relation to you, when you observe me, I should be in slow-motion. but you are moving in relation to me, so when I observe you, will you be in slow motion too?
2) Consider the following experiment. Pam and Jim are moving in a 1-dimensional space frame. Pam moves to the right with velocity v (in relation to me, I'm at rest at the origin), and Jim moves to the left with velocity v too. Both are hanging a 1 meter rule in the hands, pointing forward. They have always the same distance in relation to the origin.
Consider the following events
Event 1: the front of the Pam's rule touches Jim
Event 2: the back of the Pam's rule passes Jim
Event 3: the front of the Jim's rule touches Pam
Event 4: the back of the Jim's rule passes Pam
Δt(x,y) = time interval between event x and y measured by Pam
Δt'(x,y) = time interval between event x and y measured by Jim
Δt''(x,y) = time interval between event x and y measured by me
For me, events 1 and 3, 2 and 4 should be simultaneous. But let's analyze Jim's frame of reference. For Jim, event 1 and 2 occur at the same place, so, Jim measures the proper time. Thereby Δt(1,2) > Δt'(1,2)
Also, Δt'(3,4) > Δt(3,4)
For symmetry, Δt(3,4)=Δt'(1,2), Δt(1,2)=Δt'(3,4)
So Δt(1,2)>Δt(3,4)
and the events should not be simultaneous to Jim, the same for Pam
Is this right?