- #1
TrickyDicky
- 3,507
- 27
Under what circumstances can a conservative field NOT be irrotational?
TrickyDicky said:Under what circumstances can a conservative field NOT be irrotational?
TrickyDicky said:Under what circumstances can a conservative field NOT be irrotational?
You're mixing things up. The curl of a gradient is always zero. No matter what the domain of the vector field is. The "converse" is not generally true. That is: if the curl of a vector field is 0, then it is the gradient of something. That requires the domain to be simply connected. This last statement is essentially the Poincaré lemma.Zelyucha said:When the vector field is on a surface that is not simply connected. How is this so?
Have a look at the curl operator in matrix form:
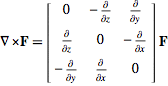
If you look closely you can see that the curl operator, which I will refer to from now on as ∇× is a skew-symmetric matrix. It turns out that the exponential map of a skew-symmetric matrix is an orthogonal matrix(its transpose is equal to its inverse). This can be shown by defining the matrix S = e∇× and ST=e-∇×. Now we take the matrix product S×ST = e∇××e-∇× = e(∇×)-(∇×) = e[0] = I3 = e-∇×+∇× = e-∇××e∇× = ST×S = I3 where [0] is the zero matrix(a 3×3 matrix of all zero entries) and I3 is the square identity matrix of dimension 3.
Now that we have shown that the exponential of ∇× is an orthogonal matrix, there's an even more detailed proof here showing that the exponential of a skew symmetric matrix like the Curl operator is a rotation matrix.
So if G is the gradient of a 3 dimensional scalar field and ∇×G = 0, then e∇×G = I3 which is the identity element of SO(3)( the group of rotations about the origin of vectors in Euclidean 3 space R3) which is itself not simply connected. So the map of all simply connected scalar fields in R3 maps to the Kernel{SO(3)} as is not 1-to-1. Whereas scalar fields in
R3 that are not simply connected map into SO(3)~I3. This map is injective but not surjective. So the curl of the gradient of a scalar field that is not simply connected corresponds to a rotation operator.
micromass said:You're mixing things up. The curl of a gradient is always zero. No matter what the domain of the vector field is. The "converse" is not generally true. That is: if the curl of a vector field is 0, then it is the gradient of something. That requires the domain to be simply connected. This last statement is essentially the Poincaré lemma.
[itex]\omega = df[/itex] hence [itex]d\omega = d(df) = d^{2}f = 0[/itex]. See how pretty it is with differential forms =D. Or you know, if you're a masochist, go ahead and work out the curl of a gradient in coordinates xD.Zelyucha said:UGH...Ya got me! iStand corrected.
But I'd like to see the proof of this if you will.
Zelyucha said:micromass, upon looking at some old notes of mine attempting to disprove that ∇×∇f = 0
for any scalar function f mapping R2 into R3 which is continuous and is differentiable up to at least order 2, I found a page which actually proves it to be correct.
One can write δ2f/δyδx = lim(Δy→0) {(f'(x,y+Δy,z) -f'(x,y,z))/Δy} and the quantity in the brackets can be re-written as lim(Δx→0){ (f(x+Δx,y,z) -f(x,y,z))/Δx}. Substituting we get:
δ2f/δyδx = lim(ΔyΔx→0) { (f(x+Δx,y+Δy,z) - f(x+Δx,y,z) + f(x,y,z))/ΔyΔx}.
and
δ2f/δyδx = lim(ΔxΔy→0) { (f(x+Δx,y+Δy,z) - f(x,y+Δy,z) + f(x,y,z))/ΔxΔy}.
Since multiplication of real numbers is commutative, ΔyΔx = ΔxΔy and if we subtract the 2 quantities in brackets we now have:
[δ2f/δyδx -δ2f/δyδx] = lim(ΔxΔy→0){ (f(x,y+Δy,z)-f(x+Δx,y,z))/ΔxΔy}
By the continuity of f: R2→R3, there is a point a = (x,y) in R2 whose image is f(x,y,z) and any open δ-neighborhood has an ε-neighborhood on G centered at Img(a) in G. So if we consider the points ax =(x+Δx,y) and ay=(x,y+Δy) in R2 and the vector X connecting them, then |X| = √(Δx2+Δy2). Now I claim that
lim(ΔxΔy→0){ (f(x,y+Δy,z)-f(x+Δx,y,z))/ΔxΔy} = 0. Which implies that for any ε > 0, there exists a δ > 0 such that:
|(f(x,y+Δy,z)-f(x+Δx,y,z))|/|ΔxΔy| < ε whenever the distance d(ax,ay) < δ. So what is the delta? Well since the vectors from a→ax and a→ay are orthogonal(to see this just set (x,y)=0), if you were to move one of those points towards the other along the X which connects them such that d(ax,ay) < √(Δx2+Δy2) = |X|, then we can choose δ = |X| and place our δ-disk at the midpoint of X between ax and y. So shrinking ε means we move the 2 a points even closer together along X to re-size our δ-disk. And as ΔxΔy→0(along with |X|), then the |Img(X)|→0 and the proof is complete. [δxiδxj]°δf = 0 whenever i≠j.
micromass said:Your proof looks more like a proof for the theorem of Clairaut-Schwarz... http://en.wikipedia.org/wiki/Symmetry_of_second_derivatives
Zelyucha said:Might I add, the fact that the Curl of the Gradient of a scalar function is always zero is a direct consequence of Clairaut's theorem since the theorem states that mixed partials commute.
But what about a continuous well defined function of differential class C2+ on real projective space? Or more specifically a scalar function f in R3 that defines a non-orientable surface?
micromass said:Of course you can calculate partial derivatives on weird manifolds. Then the partial derivatives don't necessarily commute since you can have a weird chart. You can define a Lie-bracket to see how much the partial derivatives commute.
But curl and gradient are defined completely different on manifolds. They are not longer vector fields but differential forms. The curl and gradient correspond to the exterior derivative and you can show that applying the exterior derivative twice gives 0.
Zelyucha said:A conservative vector field for this purpose is simply the gradient of a function that defines a 2-dimensional manifold embedded in R3.
So when you speak of manifolds you are speaking of a completely separate topological space whereas what I'm talking about is restricted to (2D)surfaces in Euclidean 3D space. The CURL operator is a differential 2-form on such an object.
Now consider the scalar function ψ: (x,y,z) → (x/√(x2+y2+z2),y/√(x2+y2+z2),z/√(x2+y2+z2)) = (ψ(x),ψ(z),ψ(z))
This is a mapping of R3 into Real projective space(of dimension 2). If you take ∇ψ = (δψ(x)/δx, δψ(y)/δy,δψ(z)/δz)
micromass said:I am very sorry to say that I could make very little sense of your post.
I'm not following. If you define your manifold as a level set of [itex]F:\mathbb{R}^3\rightarrow \mathbb{R}[/itex], then the gradient is a normal field on F. I don't get why you call this a conservative vector field at all.
The curl operator is not a 2-form.
You say that
[tex]\psi(x)=\frac{x}{\sqrt{x^2 + y^2 + z^2}}[/tex]
But the right hand side depends clearly on x, y and z. And the left-hand side depends on x. So the notation is not very legal.
In my knowledge, a gradient is only defined for a scalar field, that is for a sufficiently smooth function [itex]f:\mathbb{R}^3\rightarrow \mathbb{R}[/itex]. You seem to be taking a gradient for something whose codomain is not [itex]\mathbb{R}[/itex]. I don't know how that is defined.
Zelyucha said:I do realize that my notation for ψ equations was not legal. However, regarding the final paragraph, the Möbius strip is a surface whose codomain is R3 but is homeomorphic to the real projective plane. However, it is not an embedding.
Let's try this again:
[tex]\psi(x,y,z)=(\frac{x}{\sqrt{x^2 + y^2 + z^2}},\frac{y}{\sqrt{x^2 + y^2 + z^2}},\frac{z}{\sqrt{x^2 + y^2 + z^2}}) [/tex]
What am suggesting is that rule that ∇×∇f = 0 for any scalar function with domain R3 does not hold when f defines a non-orientable surface.
micromass said:What do you mean with the "codomain of a surface"??
Furthermore, do you have any reference that says that the Mobius strip is homeomorphic to the projective plane?? I find this very difficult to believe.
It's simply not true. You can actually prove that the curl of the gradient is zero for surfaces (provided we express everything as forms). And as of now, you have still not given a valid counterexample to that claim.
Your example literally makes no sense because your map doesn't even map to the reals so what does the gradient even mean in that case? Secondly, the real projective plane is compact but the Mobius strip isn't so your claim regarding them being homeomorphic is already false. Your link also never claims they are homeomorphic. I have no idea what is being attempted to be shown here.Zelyucha said:I actually worked out the ∇×∇ψ and it does not vanish. For the homeomorphism between the Mobius strip and the (Real)projective plane, look here.
WannabeNewton said:Your example literally makes no sense because your map doesn't even map to the reals so what does the gradient even mean in that case? Secondly, the real projective plane is compact but the Mobius strip isn't so your claim regarding them being homeomorphic is already false. Your link also never claims they are homeomorphic. I have no idea what is being attempted to be shown here.
WannabeNewton said:You made a calculation error somewhere along the road. Just plug it into wolfram. I got 0.
WannabeNewton said:Your example literally makes no sense because your map doesn't even map to the reals so what does the gradient even mean in that case? Secondly, the real projective plane is compact but the Mobius strip isn't so your claim regarding them being homeomorphic is already false. Your link also never claims they are homeomorphic. I have no idea what is being attempted to be shown here.
micromass said:The curl operator is not a 2-form.
Zelyucha said:FYI: The Möbius strip is compact.
However, it is not homeomorphic to the projective plane because the Möbius strip has 2 closed boundary curves whereas RP2 does not.
It actually is. Look here at the wikipedia article regarding differential forms and if you scroll down to section 4.1 there is the definition of the wedge product for a differential 2-form which is precisely what the CURL operator is for surfaces in R3. So let F be a vector field in R3. ∇×F = [(dx^dy)+(dx^dz)+(dy^dz)]°F. You can write out the CURL in matrix form and see that it is a skew-symmetric 3×3 matrix with Trace=0.
The curl of gradient is a mathematical operation that describes the rotation of a vector field at a particular point. It is calculated by taking the cross product of the del operator (∇) and the gradient (∇f) of a scalar function f.
A conservative field is one in which the work done by the field to move an object from one point to another is independent of the path taken. This means that the total work done in a closed loop is equal to zero.
A conservative field is always irrotational, meaning that the curl of gradient is equal to zero. This is because the curl of gradient measures the rotation of a vector field, and a conservative field has zero rotation.
A conservative field is not irrotational when there are forces acting on an object that cause it to rotate as it moves along a path. This means that the work done by the field to move the object from one point to another will be dependent on the path taken, making the field non-conservative.
If the curl of gradient is equal to zero, we know that the field is conservative. This is because the absence of rotation means that the field is path-independent, and the work done is equal to zero for a closed loop. Therefore, we can use the curl of gradient to test if a field is conservative or not.