mymachine
- 42
- 0
If I construct a curve such start from point A0, A3, to point A6 where A1-A2 and A4-A5 are control points, is called a Bezier curve.
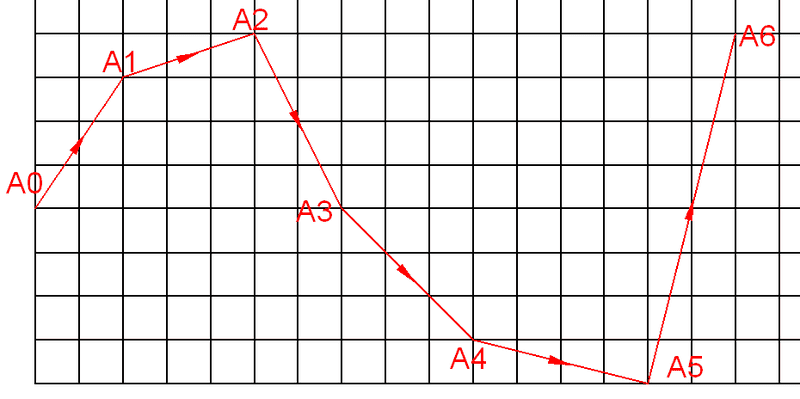
What is it called by and what its equation if I construct and fit a curve start from point A0 > A1 > A2 > A3 > A4 > A5 > A6 such as below image?
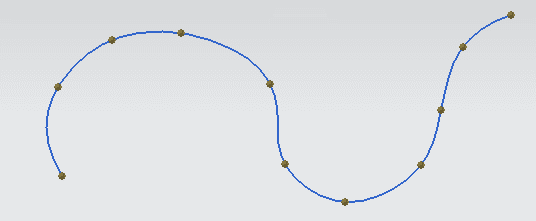
What is it called by and what its equation if I construct and fit a curve start from point A0 > A1 > A2 > A3 > A4 > A5 > A6 such as below image?
