Jhenrique
- 676
- 4
Is possible to rewrite the quadratic, cubic and quartic determinant in terms of matrices and matrix operations (trace and determinant)?
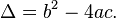
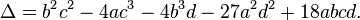
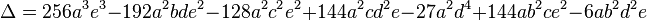
https://en.wikipedia.org/wiki/Discriminant_of_a_polynomial#Formulas_for_low_degrees
https://en.wikipedia.org/wiki/Discriminant_of_a_polynomial#Formulas_for_low_degrees