- #1
shirel
- 38
- 0
It is a nice question.
It has a few different kinds of proofes.
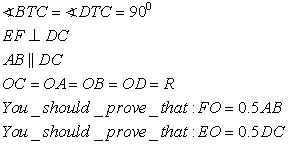
So who is smart here?
It has a few different kinds of proofes.
So who is smart here?
Last edited:
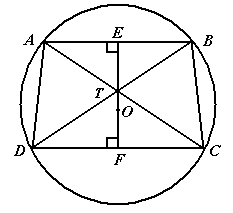
Moo Of Doom said:Clearly, neither propositions is true. For example, you can lengthen EO by moving A and B up the circle a bit without changing DC. There's no relationship between them at all.
AlephZero said:How do you do that, without changing angles BTC and DTC? (From the figure, I'm assuming ATC and BTD are straight lines, though it doesn't explicitly say that).
shirel said:Thanks...
I just couldn't find which triangles are similar..
A "smart" person in terms of geometry is someone who has a strong understanding of geometric concepts and is able to apply them to solve complex problems. This includes having excellent spatial reasoning skills, being able to visualize and manipulate shapes, and having a deep understanding of geometric principles and formulas.
To improve your geometry skills, it is important to practice regularly and consistently. This can include solving a variety of exercises and problems, as well as studying and reviewing key concepts and formulas. It may also be helpful to seek out additional resources, such as textbooks or online tutorials, to supplement your learning.
Yes, there are several strategies and techniques that can be helpful for solving geometry exercises. These include breaking down complex problems into smaller, more manageable parts, drawing diagrams or using visual aids to better understand the problem, and looking for patterns or relationships between different elements of the problem. It is also important to carefully read and understand the given information before attempting to solve the problem.
While memorizing formulas can be helpful, it is not the only factor that determines one's intelligence in geometry. It is important to understand the concepts and principles behind the formulas, and to be able to apply them in different situations. Additionally, being able to think critically and problem-solve is also crucial in geometry, rather than simply relying on memorization.
Geometry has many practical applications in everyday life. For example, it is used in architecture and construction to design buildings and structures, in engineering to create models and blueprints, and in art and design to create visually appealing compositions. Additionally, geometry is also used in navigation, mapmaking, and even in fields such as astronomy and physics to understand the world around us.