- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What should be the particular solution?
- Thread starter tony_engin
- Start date
-
- Tags
- Particular solution
In summary, Daniel is explaining that the trial particular solution for the nonhomogeneous constant coefficient ODE is "[Asinx+Bcosx+C] exp(-2x)", but this is wrong and the correct solution is "[(Asinx+Bcosx)x+C] exp(-2x)".
Physics news on Phys.org
- #2
Pyrrhus
Homework Helper
- 2,186
- 1
Yes it's ok.
- #3
- 13,349
- 3,127
Or you can do it by the method of variation of constants.I've always thought of it as being elegant...
Daniel.
Daniel.
- #4
- #5
Pyrrhus
Homework Helper
- 2,186
- 1
Yes you should try
[tex] x^{2}e^{-2x}(Ax \cos 2x + Bx \sin 2x + C) [/tex]
There are other methods for solving nonhomogenous constant coefficients ODEs such as Anulator Method by using the differential operator, and also Variation of parameters.
Here's a preview of the Anulator Method.
Imagine a ODE
[tex] y'' + 3y' + 2y = 4x^2 [/tex]
if we rewrite the above ODE with the differential operator D
[tex] (D^2 + 3D +2)y = 4x^2 [/tex]
Now if we use a differential operator [itex] D^3 [/itex] we could eliminate [itex] 4x^{2} [/itex]
[tex] D^3(D^2 + 3D +2)y = 4 D^3 x^2 [/tex]
[tex] D^3(D^2 + 3D +2)y = 0 [/tex]
Thus making a fifth grade auxiliary equation. There are more steps it was just a preview.
[tex] x^{2}e^{-2x}(Ax \cos 2x + Bx \sin 2x + C) [/tex]
There are other methods for solving nonhomogenous constant coefficients ODEs such as Anulator Method by using the differential operator, and also Variation of parameters.
Here's a preview of the Anulator Method.
Imagine a ODE
[tex] y'' + 3y' + 2y = 4x^2 [/tex]
if we rewrite the above ODE with the differential operator D
[tex] (D^2 + 3D +2)y = 4x^2 [/tex]
Now if we use a differential operator [itex] D^3 [/itex] we could eliminate [itex] 4x^{2} [/itex]
[tex] D^3(D^2 + 3D +2)y = 4 D^3 x^2 [/tex]
[tex] D^3(D^2 + 3D +2)y = 0 [/tex]
Thus making a fifth grade auxiliary equation. There are more steps it was just a preview.
Last edited:
- #6
tony_engin
- 45
- 0
For the first differential equation that I firtsly raised, the answer of the particular solution should be something like "[1+xcosx] exp(-2x)" as given by the book. So I think the trial form should not be "[Asinx + Bcosx + C] exp(-2x)", right? So, what should be the correct form?
- #7
- 13,349
- 3,127
I've already given you the hint to do it.It's up to you if u prefer other method,just as long as it leads to the result.The correct one.
Daniel.
Daniel.
- #8
tony_engin
- 45
- 0
um...you mean do it by variation of constants?
Since this is an exercise in trying the particular solution, I would like to know the form of the trial particular solution.
Since this is an exercise in trying the particular solution, I would like to know the form of the trial particular solution.
- #9
- 13,349
- 3,127
One of the solution of the homogenous one contains that e^{-2x},so that should give a hint on how to pick the trial function.
Daniel.
Daniel.
- #10
tony_engin
- 45
- 0
I previously thought that I should try "[Asinx + Bcosx + C] exp(-2x)"
but the answer given by the book shows that this is wrong..
but the answer given by the book shows that this is wrong..
- #11
- 13,349
- 3,127
Of course.You need an "x" to multiply the exponential,because the exponential is contained both in the solution of the hom.eq. and in the nonhomogeneity term.
Daniel.
Daniel.
- #12
tony_engin
- 45
- 0
So, it should be "[(Asinx + Bcosx)x + C] exp(-2x)" or "x[Asinx + Bcosx + C] exp(-2x)"?
- #13
- 13,349
- 3,127
The first without the C,it's useless there.
Daniel.
Daniel.
- #14
Pyrrhus
Homework Helper
- 2,186
- 1
If you're still referring to your ODE.
[tex] y_{p_{1}} = Ce^{-2x} [/tex]
[tex] y_{p_{2}} = xe^{-2x}(A \cos x + B \sin x) [/tex]
[tex] y_{p} = Ce^{2x} + xe^{-2x}(A \cos x + B \sin x) [/tex]
[tex] y_{p_{1}} = Ce^{-2x} [/tex]
[tex] y_{p_{2}} = xe^{-2x}(A \cos x + B \sin x) [/tex]
[tex] y_{p} = Ce^{2x} + xe^{-2x}(A \cos x + B \sin x) [/tex]
- #15
saltydog
Science Advisor
Homework Helper
- 1,591
- 3
Tony, where are you with this? Getting it?
This is what I'd do (other than just plug it into Mathematica):
I tell you what, since the RHS is a particular solution to the homogeneous ODE:
[tex](D+2)(D^2+4D+5)y=0\quad\text{(1)}\quad[/tex]
you can apply this operator to both sides of the original equation to aniliate the RHS, that is:
If you have:
[tex]y^{''}+4y^{'}+5y=e^{-2x}(1+Cos(x))\quad\text{(2)}\quad[/tex]
Applying the differential operator in (1) to both sides yields:
[tex](D+2)(D^2+4D+5)(D^2+4D+5)y=0\quad\text{(3)}\quad[/tex]
Right?
The solution of (3) will contain the solution of (2), just gets messy that's all.
So the solution of (3) is:
[tex]y(x)=c_1e^{-2x}+c_2e^{-2x}Cos(x)+c_3e^{-2x}Sin(x)+c_4xe^{-2x}Cos(x)+c_5xe^{-2x}Sin(x)[/tex]
And thus a particular solution of (2) will be:
[tex]y_p(x)=Ae^{-2x}+Bxe^{-2x}Cos(x)+Cxe^{-2x}Sin(x)[/tex]
Now what? How about a plot of the solution (just make up some initial conditions)?
This is what I'd do (other than just plug it into Mathematica):
I tell you what, since the RHS is a particular solution to the homogeneous ODE:
[tex](D+2)(D^2+4D+5)y=0\quad\text{(1)}\quad[/tex]
you can apply this operator to both sides of the original equation to aniliate the RHS, that is:
If you have:
[tex]y^{''}+4y^{'}+5y=e^{-2x}(1+Cos(x))\quad\text{(2)}\quad[/tex]
Applying the differential operator in (1) to both sides yields:
[tex](D+2)(D^2+4D+5)(D^2+4D+5)y=0\quad\text{(3)}\quad[/tex]
Right?
The solution of (3) will contain the solution of (2), just gets messy that's all.
So the solution of (3) is:
[tex]y(x)=c_1e^{-2x}+c_2e^{-2x}Cos(x)+c_3e^{-2x}Sin(x)+c_4xe^{-2x}Cos(x)+c_5xe^{-2x}Sin(x)[/tex]
And thus a particular solution of (2) will be:
[tex]y_p(x)=Ae^{-2x}+Bxe^{-2x}Cos(x)+Cxe^{-2x}Sin(x)[/tex]
Now what? How about a plot of the solution (just make up some initial conditions)?
Last edited:
- #16
saltydog
Science Advisor
Homework Helper
- 1,591
- 3
Just some follow up:
Well, if you substitute [itex]y_p(x)[/itex] into (2) above, it gets a little messy, do this and that, equate coefficients, some things cancel, and we're left with:
[tex]y_p(x)=e^{-2x}+\frac{1}{2}xe^{-2x}Sin(x)[/tex]
So that the general solution is:
[tex]y(x)=c_1e^{-2x}Cos(x)+c_2e^{-2x}Sin(x)+e^{-2x}+\frac{1}{2}xe^{-2x}Sin(x)[/tex]
Letting:
y(0)=1
y'(0)=1
we get:
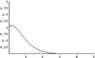
[tex]y(x)=3e^{-2x}Sin(x)+e^{-2x}+\frac{1}{2}xe^{-2x}Sin(x)[/tex]
I've attached a plot of this solution. Tony, you can do all this right?
Well, if you substitute [itex]y_p(x)[/itex] into (2) above, it gets a little messy, do this and that, equate coefficients, some things cancel, and we're left with:
[tex]y_p(x)=e^{-2x}+\frac{1}{2}xe^{-2x}Sin(x)[/tex]
So that the general solution is:
[tex]y(x)=c_1e^{-2x}Cos(x)+c_2e^{-2x}Sin(x)+e^{-2x}+\frac{1}{2}xe^{-2x}Sin(x)[/tex]
Letting:
y(0)=1
y'(0)=1
we get:
[tex]y(x)=3e^{-2x}Sin(x)+e^{-2x}+\frac{1}{2}xe^{-2x}Sin(x)[/tex]
I've attached a plot of this solution. Tony, you can do all this right?
Attachments
What should be the particular solution?
The particular solution refers to the specific solution to a problem or question. It is the answer or outcome that is unique to a particular situation.
What factors should be considered when determining the particular solution?
When determining the particular solution, it is important to consider the nature of the problem, available resources, potential consequences, and desired outcome. Other factors such as time constraints and ethical considerations may also play a role.
How can a particular solution be tested for effectiveness?
A particular solution can be tested for effectiveness through experimentation, research, and data analysis. This involves setting up controlled experiments, collecting data, and analyzing the results to determine if the solution is achieving the desired outcome.
What if the particular solution does not work?
If the particular solution does not work, it is important to reassess the problem and potential factors that may have affected the outcome. This may involve making adjustments to the solution or trying a different approach altogether. It is also important to learn from the failed solution and use that knowledge to inform future decisions.
Can the particular solution be applied to other similar problems?
In some cases, a particular solution may be applicable to other similar problems. However, it is important to carefully evaluate each situation and consider any unique factors that may affect the outcome. It may also be necessary to make adjustments to the solution in order to address the specific needs of each problem.
Similar threads
- Replies
- 52
- Views
- 814
-
Differential Equations
- Replies
- 3
- Views
- 1K
-
Differential Equations
- Replies
- 5
- Views
- 1K
-
Calculus and Beyond Homework Help
- Replies
- 7
- Views
- 501
-
Differential Equations
- Replies
- 5
- Views
- 4K
-
Differential Equations
- Replies
- 5
- Views
- 1K
-
Differential Equations
- Replies
- 2
- Views
- 4K
-
Calculus and Beyond Homework Help
- Replies
- 2
- Views
- 177
-
Differential Equations
- Replies
- 1
- Views
- 862
-
Differential Equations
- Replies
- 7
- Views
- 2K
Share: