Are String Theory Correction Terms Infintesimal under Supersymmetry Conditions?

[FalseVaccum89]

I was just reading an article on superstringtheory.com in the Black Holes section entitled "Space, Time, and String Theory" when I came across the following predicted reformulation of Einstein's tensor:

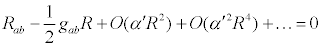
The explanation for this was as follows:

Note that string theory does not predict that the Einstein equations are obeyed exactly. Perturbative string theory adds an infinite series of corrections to the Einstein equation. . . So our understanding of spacetime in perturbative string theory is only valid as long as spacetime curvature is small compared to the string scale.
However, when these correction terms become large, there is no spacetime geometry that is guaranteed to describe the result. Only under very strict symmetry conditions, such as unbroken supersymmetry, are there known exact solutions to the spacetime geometry in string theory.

My question is this: are those correction terms just really, really small but finite, or are they infintesimal under the "very strict symmetry conditions" described?

 

[mathman]

I know nothing about the theory. However it seems that the question you are asking is simply about the relative size of the term α'R² in comparison with the leading term. My guess is small but finite is the better description.

 

[friend]

I thought I saw some generalization where derivatives of R are used in the expansion.

 

[FalseVaccum89]

I know nothing about the theory. However it seems that the question you are asking is simply about the relative size of the term α'R² in comparison with the leading term. My guess is small but finite is the better description.

Thank you for your reply,

I'm leaning towards finite, but small as well. The only thing is, on page 53 of A First Course in String Theory (1st ed), Barton Zwiebach says there can be an "infinitesimal change of the metric. . .", referring to Einstein's Tensor in this case, which makes me wonder if the correction terms might be infinitesimal when certain symmetries aren't broken. It seems logical to me that when those terms do become finite (should that be the case), the resultant infinite changes in the metric would cause there to be "no spacetime geometry that is guaranteed to describe the result."

I'm probably off base on this somewhere, though, because I'm not at a level to handle the formalism yet. :P



FV89

 

[LBloom]

FV89,

There are two different things at play here. Whats on the superstring theory website is about possible corrections to Einsteins theory of gravity that are predicted by String Theory. String Theory should reproduce GR in the low energy limit (theres the natural appearance of the graviton), but with the graviton also comes the dilaton. The dilaton is a scalar field that controls coupling constants. What String Theory should predict is a scalar-tensor theory of gravity, Brans-Dicke theory I believe, which also reproduces GR in certain limits.

The idea is that there are perturbative corrections that are supressed by factors of alpha and R (when R is small), but when R is large enough we can't ignore these factors anymore and classical GR breaks down.

In Zwiebach's book he's referring to something different. Here he's working with purely classical GR and he's exploiting the general coordinate (diffeomorphism) invariance of GR, which acts like a gauge invariance. Its just like in electromagnetism where there's a the gauge invariance is a phase and we can choose a particular gauge.

Here you should think about the metric tensor like you would think about any other vector or tensor field. If I have a vector and I change my coordinates by a 90 degree rotation I expect that the coordinates of my vector will change (it stays fixed I move the axes). If I had an infinitesimal change in the coorindates, the components should also transform (by some small amount). This idea generalizes to tensors of arbitrary size. The change in the metric (infinitesimal or otherwise) doesn't matter in this case because its a gauge transformation and changing the gauge doesn't change the physics.

So to summarize, what you had originally refers to a new theory of gravity where perturbative terms are surpressed due to their small size and we don't notice them. What Zweibach refers to is the general, classical gauge invariance of GR.

Hope that helps!

 

[FalseVaccum89]

FV89,

There are two different things at play here. Whats on the superstring theory website is about possible corrections to Einsteins theory of gravity that are predicted by String Theory. String Theory should reproduce GR in the low energy limit (theres the natural appearance of the graviton), but with the graviton also comes the dilaton. The dilaton is a scalar field that controls coupling constants. What String Theory should predict is a scalar-tensor theory of gravity, Brans-Dicke theory I believe, which also reproduces GR in certain limits.

Now I know what the dilaton is! :D From what you've just told me, it almost sounds like some physicist was being a bit snarky with the name--it sounds like a pun.

Funnies aside, if the dilaton always comes with the graviton, and it controls coupling constants, then I'm thinking one could argue that in some sense the coupling constants are emergent from the properties of spacetime itself.

The idea is that there are perturbative corrections that are supressed by factors of alpha and R (when R is small), but when R is large enough we can't ignore these factors anymore and classical GR breaks down.

In Zwiebach's book he's referring to something different. Here he's working with purely classical GR and he's exploiting the general coordinate (diffeomorphism) invariance of GR, which acts like a gauge invariance. Its just like in electromagnetism where there's a the gauge invariance is a phase and we can choose a particular gauge.

Makes sense. I'm definitely going to have to pay attention to that when I read his book in full. (I've got an ebook copy of the second edition.)

Here you should think about the metric tensor like you would think about any other vector or tensor field. If I have a vector and I change my coordinates by a 90 degree rotation I expect that the coordinates of my vector will change (it stays fixed I move the axes). If I had an infinitesimal change in the coorindates, the components should also transform (by some small amount). This idea generalizes to tensors of arbitrary size. The change in the metric (infinitesimal or otherwise) doesn't matter in this case because its a gauge transformation and changing the gauge doesn't change the physics.

So to summarize, what you had originally refers to a new theory of gravity where perturbative terms are surpressed due to their small size and we don't notice them. What Zweibach refers to is the general, classical gauge invariance of GR.

Annnnd, I should have seen that one for myself. No worries, though, I do now.

Hope that helps!

Your reply not only answered my question, it got me thinking in a couple of directions I hadn't thought of before. Thank you.

Cheers!

FV89

 

[haushofer]

Basically, the dynamics of the string vibrations are governed by the fact that conformal invariance must be retained, hence that the beta function of the two-dimensional CFT vanishes. This puts constraints on the string vibrations on the worldsheet, which can be translated into constraints on spacetime: the equations of motion. One of these constraints implies the vacuum field equations of GR.