- #1
Orion1
- 973
- 3
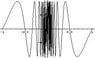
My calculus book describes the following example:
Equation:
[tex]\lim_{x \rightarrow 0} \sin \frac{\pi}{x} = \text{does not exist}[/tex]
However, my independent research indicates that it is actually:
Equation:
[tex]\lim_{x \rightarrow 0} \sin \frac{\pi}{x} = \text{Interval}(-1,1)[/tex]
Is this second solution only theoretical, and not a real valid solution in a Calculus I course?