- #1
clairez93
- 114
- 0
Homework Statement
[tex]\int^{4}_{0}\int^{(4-x)/2}_{0}\int^{(12-3x-6y)/4}_{0}dz*dy*dx[/tex]
Rewrite using the order dy dx dz.
Homework Equations
The Attempt at a Solution
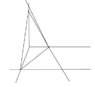
I have it graphed, but from here, I am having a hard time visualizing the bounds of all these dimensions to reorder the integral. My graph is attached.
The only thing I can determine for sure is that the bounds in the z direction will be 0 to 3. The book's answer is this:
[tex]\int^{3}_{0}\int^{(12-4z)/3}_{0}\int^{(12-4z-3x)/6}_{0}dy*dx*dz[/tex]
I can somewhat make sense of the dy bound; they solved the z equation in terms of y, although I can't really see/visualize the reason for this.
I don't understand the x bound at all, why does the y part disappear? It seems they solved the z equation to get it in terms of only z but I don't see why the y component disappears, or why they would even do that in the first place.