clope023
- 990
- 130
[SOLVED] Riding a Loop the Loop (velocity at the bottom of the loop)
A car in an amusement park ride rolls without friction around the track shown in the figure. It starts from rest at point A at a height h above the bottom of the loop. Treat the car as a particle.
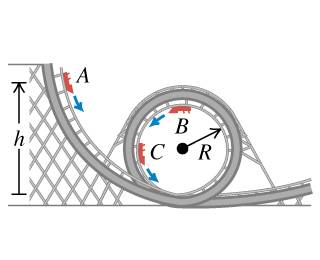
part A - What is the minimum value of h (in terms of R) such that the car moves around the loop without falling off at the top (point B)?
found this to be 5/2R, since:
sigma Fy = Fc - N - mg = 0
N = 0 and Fc = mv^2/R
so Fy = Fc = mg and mv^2/R = mg and v^2 = GR
h = (1/2mgR + 2mgR)/mg = 1/2R + 2R = 5/2R
now I'm stuck on the velocity at the point C.
part B - If the car starts at height h = 4.50 R and the radius is R = 22.0m , compute the speed of the passengers when the car is at point C, which is at the end of a horizontal diameter.
mgR = 1/2mv^2
v^2 = \sqrt{2mgR}
got v = 29 which was wrong, I might be using the wrong formulas or the wrong radius, or the formulas in the wrong way; this is an energy conservation problem.
any help is appreciated.
Homework Statement
A car in an amusement park ride rolls without friction around the track shown in the figure. It starts from rest at point A at a height h above the bottom of the loop. Treat the car as a particle.
part A - What is the minimum value of h (in terms of R) such that the car moves around the loop without falling off at the top (point B)?
found this to be 5/2R, since:
sigma Fy = Fc - N - mg = 0
N = 0 and Fc = mv^2/R
so Fy = Fc = mg and mv^2/R = mg and v^2 = GR
h = (1/2mgR + 2mgR)/mg = 1/2R + 2R = 5/2R
now I'm stuck on the velocity at the point C.
part B - If the car starts at height h = 4.50 R and the radius is R = 22.0m , compute the speed of the passengers when the car is at point C, which is at the end of a horizontal diameter.
Homework Equations
mgR = 1/2mv^2
v^2 = \sqrt{2mgR}
The Attempt at a Solution
got v = 29 which was wrong, I might be using the wrong formulas or the wrong radius, or the formulas in the wrong way; this is an energy conservation problem.
any help is appreciated.
Last edited: