Gabor888
- 1
- 0
Hello
I have a little problem with bezier curve. There is a bezier curve, with n degree, with some control points. And the problem is, that i want to know the t, and i know the y of that point. So there's a curve, in this curve there is a point, i know that place, and i want to know, what is t in this bezier.
With this algorithm(which i attached) i know the point, if i know the t
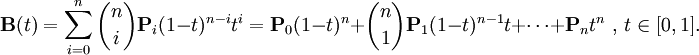
but reverse?
i know, that the t can be more numbers. I want just one of them...
I have a little problem with bezier curve. There is a bezier curve, with n degree, with some control points. And the problem is, that i want to know the t, and i know the y of that point. So there's a curve, in this curve there is a point, i know that place, and i want to know, what is t in this bezier.
With this algorithm(which i attached) i know the point, if i know the t
but reverse?
i know, that the t can be more numbers. I want just one of them...