Prove Idntity - Dirac Delta - Distributions

Drazick
Messages
10
Reaction score
2

Homework Statement


The Identity to prove:
vid7j7.png


Homework Equations


Using Integration by parts



The Attempt at a Solution


I couldn't produce the denominator.
 
Physics news on Phys.org
Hi Drazic, welcome to PF!:smile:

Drazick said:

Homework Statement


The Identity to prove:
vid7j7.png


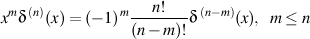
Homework Equations


Using Integration by parts



The Attempt at a Solution


I couldn't produce the denominator.

Post your calculations, and we'll be able to help.
 
I solved more general identity.
I'll post it later.
 

Thread 'Prove that the integral is equal to ##\pi^2/8##'

Prove $$\int\limits_0^{\sqrt2/4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx = \frac{\pi^2}{8}.$$ Let $$I = \int\limits_0^{\sqrt 2 / 4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx. \tag{1}$$ The representation integral of ##\arcsin## is $$\arcsin u = \int\limits_{0}^{1} \frac{\mathrm dt}{\sqrt{1-t^2}}, \qquad 0 \leqslant u \leqslant 1.$$ Plugging identity above into ##(1)## with ##u...
View full post »

Similar threads

Sifting property of a Dirac delta inverse Mellin transformation
Replies
31
Views
4K
Mellin transform of Dirac delta function ##\delta(t-a)##
Replies
3
Views
3K
Heat Kernel at t=0: Dirac Delta Intuition
Replies
3
Views
2K
Insights What Exactly is Dirac’s Delta Function? - Insight
Replies
5
Views
199
Valid Representation of Dirac Delta function
Replies
6
Views
2K
Proving a Dirac delta property
Replies
4
Views
2K
Why do integrals featuring Dirac deltas equate to certain values?
Replies
11
Views
2K
How Does the Dirac Delta Function Apply to Trigonometric Integrals?
Replies
7
Views
2K
I What Are Common Misconceptions About the Dirac Delta Function?
Replies
25
Views
3K
Dirac delta function proof fourier space
Replies
5
Views
1K

Hot Threads

Recent Insights

Back
Top