- #1
bluesunday
- 8
- 0
The time evolution operaton may be written formally as:
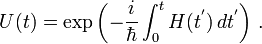
This is an actual solution to:
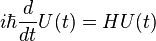
only in the case that [H(t1),H(t2)]=0 (that is: the hamiltonian commutes in different instants of time) Of course, this includes the case of a time independent hamiltonian.
If this is not the case, the actual U(t) may be obtained with the Dyson series.
This is what is stated in Sakurai, for example. But I don't really understand WHY you cannot use the exponential form of U(t) in case the Hamiltonian doesn't commute at different times. I guess it may have something to do with its integrability, but I don't know.
Any hints?
This is an actual solution to:
only in the case that [H(t1),H(t2)]=0 (that is: the hamiltonian commutes in different instants of time) Of course, this includes the case of a time independent hamiltonian.
If this is not the case, the actual U(t) may be obtained with the Dyson series.
This is what is stated in Sakurai, for example. But I don't really understand WHY you cannot use the exponential form of U(t) in case the Hamiltonian doesn't commute at different times. I guess it may have something to do with its integrability, but I don't know.
Any hints?
Last edited: