1 pulley with mass, 1 mass on the cord, 1 external force, no gravity

[andrewkirk]

I remember, a few weeks ago, when looking for homework problems I could help with, seeing one as described in the title. I couldn't think of an easy solution and was busy at the time so i made a mental note to think about it later. I finally got around to doing that yesterday, and brushed up on d'Alembert's principle, which I thought should help. But when I wrote down equations my systems were always underdetermined. My tentative conclusion was that the mass on the cord might not move at all and the cord would go slack between the block and the pulley.

I went back to look for the problem to see if I'd remembered it right. I couldn't find it, even though I searched all pulley problems on the site since late May. Maybe I dreamed it! Anyway, here's the problem, which I find intriguing. I'd value suggestions on how to approach it.

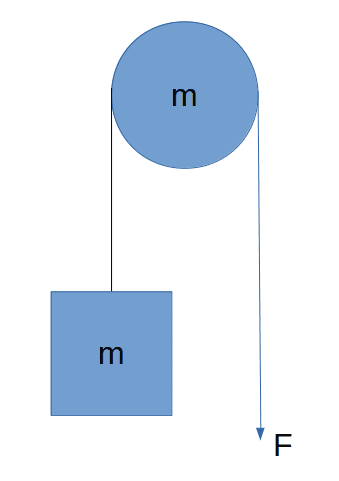
In the diagram, the cord is pulled with force F in the direction shown. Both the pulley and the square block have mass m. The cord cannot slip over the surface of the pulley (eg very high coefficient of static friction between cord and pulley). There is no gravity, and pulley and block are under no constraints other than those applied by the cord. I think of this as a plan view (ie from above) of a cylinder and cube on a frictionless ice rink.

From a high level, I expected the force F to do three things: accelerate the pulley downwards (on the page, but remember there is no real 'down' because there is no gravity), start the pulley rotating clockwise, and accelerate the block upwards. I wrote some equations but, as I said, they were underdetermined. I had one more unknown than equations.

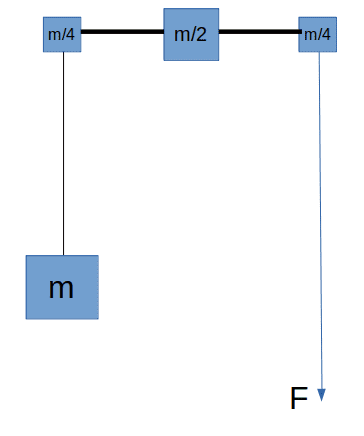
I then tried to simplify by converting the pulley to a system of three smaller blocks on a massless, rigid rod, with the same moment of inertia and combined mass as the pulley. See diagram below. But my system was still underdetermined and my tentative expectation was that the biggest block would not move. I would expect all three masses on the rod to move down, the rightmost one by the biggest distance and the leftmost one by the least.

This got me wondering what would happen if we removed the block from the problem since, if it does not move, it exerts no force on the cord or pulley. I also wondered what would happen if the two masses were different. My intuition is that if the pulley mass is much greater than that of the block, the block will be pulled upwards, but that if the block is much more massive than the pulley, the pulley would be pulled down and have no impact on the block. But that didn't make sense because it suggests a discontinuous relationship between the ratio of masses and the acceleration of the block.

By the way, if anybody remembers seeing this problem in the homework section, please post a link, as I'd love to see what responses people gave. But maybe I dreamed the whole thing!

 

[jrmichler]

My intuition is that if the pulley mass is much greater than that of the block, the block will be pulled upwards, but that if the block is much more massive than the pulley, the pulley would be pulled down and have no impact on the block. But that didn't make sense because it suggests a discontinuous relationship between the ratio of masses and the acceleration of the block.

Your intuition is correct when the mass difference is very large, although the relationship is continuous. If the two effective masses are roughly equal, they will both move.

This is very close to a real world problem that I once spent some time working on. Look up dancer roll, then US Patent 7,302,781. Below is Figure 6 from that patent:

The web 112 is pulled into the machine by pull rolls 186 and 188. That paper is accelerated from a dead stop to 200 in/sec in an inch or two of sheet travel. Roll 176 cannot possibly accelerate that fast, so the acceleration is limited to the dancer roll 274, the pull rolls, and the length of paper from the dancer roll to the machine. Even a dancer roll made from a thin wall carbon fiber tube had significant inertia, comparable to the inertia from the length of web under acceleration.

I forget exactly how I calculated the force to move the dancer. I think I just added the force on the web due to torque from angular acceleration to the force of linear acceleration due to translation. The machine worked as it was designed to work, so the calculations were, if not completely correct, good enough.

When I analyzed problems that involved simultaneous translation and rotation, my general approach was to express all forces and torques to a common point. In the above case, the common point was the total tangential force on the pull rolls. That force was directly usable for calculating the nip force between the pull rolls and the necessary drive torque.

The problem in the OP has one cord with two different tensions. One tension moves the mass, the difference between the two tensions moves and rotates the pulley. I think the easiest solution would start by calculating the rotational inertia of the pulley about an instantaneous center located at the tangent point of the cord to the mass.

 

[anuttarasammyak]

Summary:: Not sure I have the right way of thinking about this strange problem involving a free-to-move pulley and no gravity.
In the diagram, the cord is pulled with force F in the direction shown. Both the pulley and the square block have mass m. The cord cannot slip over the surface of the pulley (eg very high coefficient of static friction between cord and pulley). There is no gravity, and pulley and block are under no constraints other than those applied by the cord. I think of this as a plan view (ie from above) of a cylinder and cube on a frictionless ice rink.

Say impulse F△t acts for short time $\triangle t$. In case there is no block, the pulley gets momentum $F\triangle t$ and angular momentum $F\triangle t\ r$ around its center where r is radius of the pulley.

Attach the block.
pulley momentum: $(F+f)\triangle t$
pulley angular momentum around its center: $(F-f)\triangle t\ r$
block momentum: $-f\triangle t$
where f is force between the pulley and the block and has same direction with F.

Then how shall we know f ? Energy conservation would tell us of it.
$F\triangle x$=translation kinetic energy of the pulley + rotation kinetic energy of the pulley + translation kinetic energy of the block
where $\triangle x$ is pulling length of the rope during time interval $\triangle t$.

 

[Delta2]

I believe this thread deals with a very similar problem
https://www.physicsforums.com/threads/pulling-a-cylinder.990540/#post-6359284

 

[A.T.]

My intuition is that if the pulley mass is much greater than that of the block, the block will be pulled upwards, ...

To pull the block upwards the pulley has to rotate, so it also depends on how the pulley mass is distributed (moment of inertia).

 

[anuttarasammyak]

Further calculation of post #6
Formula of momentum
$$P=m_p\ v_p \ + m_b \ v_b$$
Formula of energy
$$PV=\frac{1}{2}m_p\ v_p^2\ + \frac{1}{2}m_b\ v_b^2\ + \frac{1}{2}I\ \omega^2$$
Formula of engular momentum
$$(P-m_b\ v_b)r=I\ \omega$$
where
P is impulse given by pulling code
V is speed pulling the code
$m_p,m_b$ are mass of pulley, block
r is radius of pulley
I is momentum inertia of pulley
$\omega$ is angular velocity of pulley rotation
$v_p,v_b$ is velocity of pulley, block with same direction of F.

We will get $v_p,v_b,\omega$ by these formula.

 

If the velocity of the string on the left side is $v_{s} \hat{y}$ and the velocity of the edge of the pulley on the left side is $(v_{p} + r\omega) \hat{y}$, where $v_{p}$ is the velocity of the centre of the pulley, then we can equate them and differentiate to obtain $a_{s} = a_{p} + r\alpha$.

If the tension on the left side is $T$ then we also have that $T = ma_{s}$, $-(T+F) = ma_{p}$ and finally also $(F-T)r = I_{p} \alpha$. If you know $I_{p}$ then I think that is a determined system.

 

[andrewkirk]

Thanks for all the replies.

I think I understand now where I went wrong. I was dividing the applied force into three parts, one to translate the pulley, one to rotate it and one to pull the block. It seemed to me too much like a perpetual motion machine that the same component of the applied force could cause both translation and rotation, rather than two parts that add to the whole applied force. Why is it that an applied force can either just cause translation - if the object to which the force is applied cannot rotate - or translation plus rotation - if the object can rotate. It sounds like in the second case the force does more, despite being the same force.

The answer is in asking more what? If we say it's more work then we can see the answer: in the second case, although the force is the same, it is applied over a greater distance. The cord travels further thru the hands of the person pulling it because the velocity of the RH tangent point of the pulley towards the puller is higher, being the sum of the translational and rim-rotational velocities. So although the force is the same, higher power is required from the puller. That put to rest my intuitive concern that we would get something from nothing.

Once I got past that hurdle, the problem becomes quite easy, using the approach of anuttarasammyak:

Let $x$ be position of block (downwards on page is positive), $y$ the position of centre of mass of pulley and $\theta$ the cumulative clockwise rotation of pulley. Then, assuming the pulley is a cylinder with moment of inertia $mr^2/2$ we have equations:

$$m\ddot y = F - m\ddot x$$
for translation of pulley from forces applied to it
$$Fr + m\ddot x r = \ddot\theta mr^2/2$$
for rotation of pulley from applied torques, and
$$ \ddot y - \ddot x = r\ddot \theta$$
from cord being unstretchable and not slipping.

Solving these three equations for the three unknowns $\ddot x,\ddot y,\ddot\theta$ gives:
$$\ddot y = \frac54\frac Fm$$
$$\ddot x = -\frac14\frac Fm$$
$$\ddot\theta = \frac64\frac Fm\frac1r$$
So that the rim rotational acceleration is
$$r\ddot\theta = \frac64\frac Fm$$
and the acceleration of the cord through the hands of the puller is $\ddot y$ plus the rim rotational acceleration, which is
$$\frac{11}4\frac Fm$$
That is nearly three times what it would be if the pulley could not rotate so, although the force is the same in both cases, the required power is far higher.

EDIT 4/7/20 changed all signs of $\ddot x$ because I realized I had written the equations as if $x$ was measured with positive being upwards direction, not the downwards direction as I said above. This correction changes the equations but not the conclusion. Note that $\ddot x$ is negative, while $\ddot y$ and $\ddot\theta$ are positive.

 

[anuttarasammyak]

Your result says some acceleration is more than F/m. It is not anticipated.
I would do some change on your equations, say x and y have same positive direction with F and θ clockwise,
$$m\ddot{y}−m\ddot{x}=F$$
$$Fr+m\ddot{x}r=\frac{mr^2}{2}\ddot{\theta}$$
$$r\ddot{θ}=\ddot{(2y−x)}$$
The first two equations and the third seem contradict. I am afraid whether "acting force F" and "pulling code tightly" are compatible.

 

[andrewkirk]

Your result says some acceleration is more than F/m. It is not anticipated.

Yes, I certainly was surprised by the result. But I'm pretty confident in it now - although happy to be corrected. I think the pulley/cylinder accelerates faster than F/m because it has force F/m applied by the puller of the cord and F/4m by the reactionary force from the accelerating block: total acceleration 5F/4m.

Noting that both x and y measure direction downwards on the page, so that $\ddot x$ is negative and $\ddot y$ is positive, I would not agree with the sign of $m\ddot x$ in your first equation, because the block is pulling the pulley downwards as a reaction because the block is accelerating upwards. I also would not agree with the factor of 2 in the third equation.

I note that in the other thread - which I didn't find because I was searching for 'pulley' while that thread calls it a 'cylinder' (thread is here, thanks @Delta2 for finding that!) - they concluded the acceleration of the block is F/4m, which agrees with my tentative result.

Another thing I just noticed: The acceleration of the block and pulley considered as a combined system is
$$\frac{m\ddot x + m\ddot y}{m+m} = \frac Fm\cdot \frac{-m\frac 14 + m\frac 54}{m+m}
= \frac F{2m}$$
which is exactly the acceleration we expect for a system of mass $2m$ when a force $F$ is applied to it. So we can think of the applied force as (1) accelerating the centre of mass of the block-and-pulley system at the expected rate $F/2m$, plus (2) moving the block and pulley closer to each other, plus (3) rotating the pulley.

What do you think?

 

[anuttarasammyak]

Thanks for your comment. I checked calculation as attached for general parameters of mass of pulley, mass of block and inertia of momentum of pulley. It seems natural but any of your checks/comments are highly appreciated.

 

@anuttarasammyak I am not sure that there should be a factor of $2$ in your no-slip condition:

Here we have $l_1 = \Delta x_p + (l_1 - \rho \Delta \theta ) + (- \Delta x_b) \implies \rho \Delta \theta = \Delta x_p - \Delta x_b$

We could also get this by considering that the velocity of the string attached to the block, $v_b$, has to equal the velocity of the edge of the pulley $v_p - \rho \dot{\theta}$ just before they make contact, i.e. $v_b = v_p - \rho \dot{\theta}$. Which would imply $\rho d\theta = dx_p - dx_b$.

I might have made a mistake, in which case, sorry in advance

 

[haruspex]

Your result says some acceleration is more than F/m. It is not anticipated.

It's mechanical advantage.
Change the set up so that the block is fixed and the cylinder smooth. You now have tension F throughout the string. a=2F/m.

 

[anuttarasammyak]

@anuttarasammyak I am not sure that there should be a factor of 2 in your no-slip condition:

I count double as I draw on your sketch.

 

I count double as I draw on your sketch.

We can imagine taking the slack, $2\Delta x_p - \Delta x_b$, and attaching it to the side on which the force is applied. However, of this length of slack, $\Delta x_p$ was already on this lower side, so the net increase in length of the lower side is only $\Delta x_p - \Delta x_b$, which must then equal $\rho \Delta \theta$. So I don't think we should double count

 

@anuttarasammyak The length of rope transferred around the pulley (from one side to the other) is $\rho \Delta \theta$. As we can see below, this is also $\Delta x_p - \Delta x_b$, so I don't think we need to double count. Note that the red section is redundant, since it is on the same side of the pulley in both snapshots:

 

[anuttarasammyak]

@ethoteipi Now I get your point and know you are right.
I would revise post #11 as attached. Now I know the code is kept tight in most cases.
Thank you so much.