- #1
gibberingmouther
- 120
- 15
i'm trying to review calculus and look a little deeper into proofs/derivations/etc. I'm doing this both for fun and to review before i go back to school.
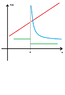
am i the only one who has difficulty understanding the "rigorous" definition of the limit? i found this web page: http://tutorial.math.lamar.edu/Classes/CalcI/DefnOfLimit.aspx
i think i can get this if i spend some more time with the explanations and exercises on this page. my question is, are there lots of hard to understand pieces of logic like this in advanced calculus or analysis? i don't have to take analysis for my degree but i want to learn a little bit of it just to expand my understanding of how the universe works (which is fun).
when i took calculus i pretty much worked through the textbook and i remember having difficulty with the definition of the limit in that book as well. for those who have taken analysis, i guess, what is it like? what can you say about it to someone with beginner/intermediate level experience like myself? i remember reading that Andrew Wile's proof of Fermat's Last Theorem was over 100 pages long. is there anything in advanced calculus like that, or are the main theorems relatively easy to demonstrate?
also, any tips on how to understand this epsilon delta thing would be appreciated.
edit: maybe the super scientists of the future will be AIs? apparently there are some super long proofs that were done by computers - not really AIs, but sophisticated programs. this got me thinking so i did some google searches.
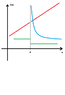
am i the only one who has difficulty understanding the "rigorous" definition of the limit? i found this web page: http://tutorial.math.lamar.edu/Classes/CalcI/DefnOfLimit.aspx
i think i can get this if i spend some more time with the explanations and exercises on this page. my question is, are there lots of hard to understand pieces of logic like this in advanced calculus or analysis? i don't have to take analysis for my degree but i want to learn a little bit of it just to expand my understanding of how the universe works (which is fun).
when i took calculus i pretty much worked through the textbook and i remember having difficulty with the definition of the limit in that book as well. for those who have taken analysis, i guess, what is it like? what can you say about it to someone with beginner/intermediate level experience like myself? i remember reading that Andrew Wile's proof of Fermat's Last Theorem was over 100 pages long. is there anything in advanced calculus like that, or are the main theorems relatively easy to demonstrate?
also, any tips on how to understand this epsilon delta thing would be appreciated.
edit: maybe the super scientists of the future will be AIs? apparently there are some super long proofs that were done by computers - not really AIs, but sophisticated programs. this got me thinking so i did some google searches.
Last edited: