About groups and continuous curves

[LCSphysicist]

TL;DR Summary

Lorentz transformations
Homomorphism
Determinant
Continuous curve

Define $$\phi(A)$$ a transformation which, acting on a vector x, returns $$AxA^{*}$$, in such way that if A belongs to the group $$SL(2,C)$$, $$||\phi(A)x||^2 = ||x||^2$$, so it conserves the metric and so is a Lorentz transformation. $$\phi(AB)x = (AB)x(AB)^{*} = ABxB^{*}A^{*} = A(BxB^{*})A^{*} = \phi(A)\phi(B)x$$ so we have homomorphism too. Now:

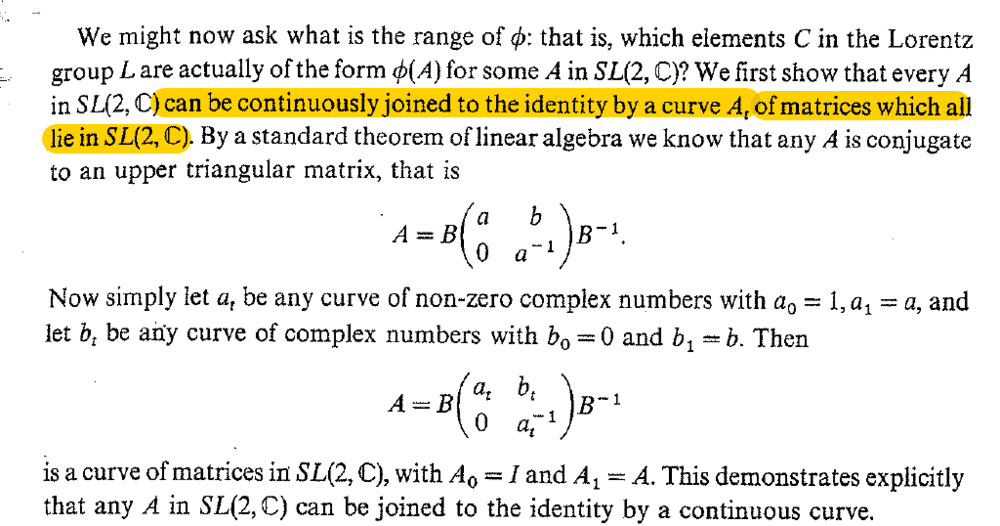
What does it means by "be continuously joined to the identity by a curve A of matrices"? It is a geometric interpretation of what? What is the meaning of curve here? I don't get this proof

 

[pasmith]

There is a natural topology on $SL(2, \mathbb{C})$: regard a 2x2 matrix with complex entries as a vector in $\mathbb{C}^{4}$ and use the toplogy induced by the standard inner product (which is equivalent to the topology induced by any norm on $\mathbb{C}^4$). A continuous curve from $A$ to $B$ in $SL(2,\mathbb{C})$ is then a function $f: [0,1] \to SL(2,\mathbb{C})$ with $f(0) = A$ and $f(1) = B$ which is continuous with respect to this topology.

 

[Stephen Tashi]

What is the meaning of curve here?

You could think of a curve in the space of 2x2 matrices with complex entries as function that maps a real valued parameter $t$ to a matrix of the form:
$C(t) = \begin{pmatrix} c_{1,1}(t)&c_{2,2}(t) \\ c_{2,1}(t)&c_{2,2}(t) \end{pmatrix}$

where each $c_{i,j}$ is a continuous function (using the definition of "continuous function" that is appropriate for complex valued functions).

A curve in the space $SL(2,\mathbb{C})$ must also satisfy the condition that $C(t) \in SL(2,\mathbb{C})$ for each value of the parameter $t$.

What does it means by "be continuously joined to the identity by a curve A of matrices"?

It means for each matrix $M \in SL(2,\mathbb{C})$ we can find a curve $C(t)$ in $SL(2,\mathbb{C})$ such that $C(0) = I$ and $C(1) = M$

I don't get this proof

I don't like the notation it uses. A clearer way to denote things is that we can express $M$ as $B \begin{pmatrix} c&d\\0&1/c\end{pmatrix} B^{-1}$.

We assert we can find continuous complex valued functions $a(t), b(t)$ such that
$a(0) = 1, a(t) =c,\ b(0) = 0, b(1) = d$
and such that for $0 \le t \le 1$ the matrix
$C(t) = B \begin{pmatrix} a(t) & b(t) \\ 0 & 1/a(t) \end{pmatrix} B^{=1}$
is in $SL(2,\mathbb{C})$. (For example, we can let $a(t)$ ever be zero.)

This constructs a curve $C(t)$ in $SL(2,\mathbb{C})$ such that $C(0) = B^{-1}IB = I$ and $C(1) = M$.

It is a geometric interpretation of what?

I don't have a good grasp of geometry in the space of complex valued 4-tuples! To me, geometry in higher dimensional spaces is only understandable in terms of algebra - as a generalization of the algebraic forms of things used to describe geometry in lower dimensional spaces.