Adding random numbers: Tolerance analysis

[Juanda]

TL;DR Summary

I want to find the probability of adding random numbers with the result being within a certain bracket.

I am not a fan of random and statistics. I know it is extremely useful and probably the mathematical branch more applicable to real life to understand the world around us but I am a Calculus and Vectors boy. This problem though I find interesting. I would like to find a generalized solution for the following situation. It is related to the study of the tolerances in manufacturing. I am certain it's got more applications but that's how it occurred to me. To be honest, I don't think I will be able to apply this in real life because I don't have access to the probability distributions (although I could make some educated guesses) but the problem is still interesting.

Let's say we are adding two numbers. The result is simple.
$$2+3=5$$
However, let's now think of a scenario where 2 and 3 are not set. Instead, they follow a probability distribution. To start with something simple, let's assume they are constant distributions as shown.

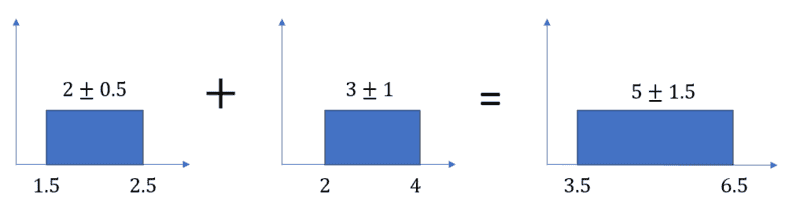
In this case, I believe that's right so I know how to do it.
$$(2\pm 0.5)+(3\pm 1)=5\pm 1.5$$
But if the probability distributions get more complex I do not know how I could try to solve it. For example:

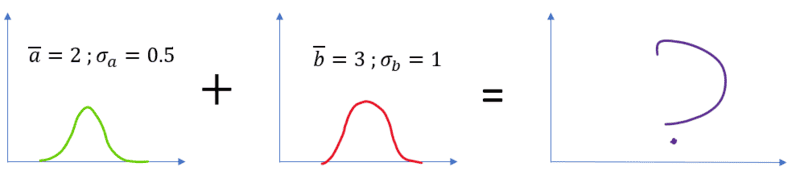
I used a normal distribution but I am certain there must be a generalized way to calculate it for any given probability distribution. I am interested in being able to answer the following:
Given the number $a$ with this probability distribution (whichever) and the number $b$ with this probability distribution (whichever), what is the probability that the sum c falls within the numbers $e$ and $d$.
Similarly, the following question would be interesting to answer:
Given the target of the number $c$ being within the limits caused by $e$ and $d$ with a 95% certainty, how should $a$ and $b$ be given that they follow this probability distribution (whichever)?
This second question would look a lot like what a designer would need to face when choosing the tolerances of machined parts. The first one allows us to check if what was chosen is right. The second one is like trying to find the best answer directly.
I am aware that the second question has infinite solutions because the problem is not sufficiently defined. I don't know how to restrain it a little more so it is still realistic and will spit out the best possible solution directly. I would guess an additional restraint would be to force the tolerance brackets to be as big as possible in both numbers so the parts are easier to manufacture. "Big" is relative, so I would define big as a percentage of the average.

As a last bonus question, I mentioned at the top of the post that the applicability of this is limited by the actual knowledge of the probability distributions present in machined parts. Let's imagine I ask for 100 cylinders to be machined to 50±0.5 mm in diameter. I believe the machinist will keep removing material with his lathe until he's within the tolerance bracket. He has no particular interest in giving me the part being as close to the nominal value as possible since that risks scrapping a part because he removed more material than necessary. Therefore, my current guess is that the distributions must look somewhat like this:

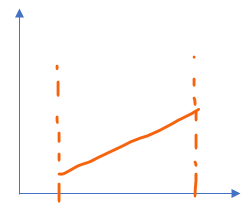
That is only an educated guess in which even psychology is involved. The machinist might be somewhat of a perfectionist and he wants to get close to the average value. The only way to know would be to take all manufactured parts and get the probability distribution but that implies the job is already done so you cannot modify the tolerance bracket in the design to nail the target you initially had in mind. Is there a best way to approach this? What probability distribution would you apply?

So far, all my work is in low volumes so even if I knew the details of this problem there is little chance they would be representative enough to apply it but I still think it's an interesting matter to think about and it might be more useful in the future. Knowledge is power.

Let me know your thoughts.
Thanks in advance.

 

[FactChecker]

The general equation for the variance of a linear combination of two random variables, $X,Y$, is
$Var(aX+bY) = a^2\ Var(X) + b^2\ Var(Y) + 2 a b\ Cov(X,Y)$, where $a, b \in R$.

 

[WWGD]

You may also be interest in Chebyshev's_inequality
https://en.m.wikipedia.org/wiki/Chebyshev's_inequality

 

[Juanda]

I am sorry but I don't understand your replies. They are either too general and I cannot make the connection to the problem at hand or they are not too related.

I kept checking the matter on the internet and thankfully I found a video that covered the point in detail. It is from the wonderful channel 3Blue1Brown and it is about convolution.


It actually bothers me a little that I watched this video when it was published but I didn't really understand it that well back then. Now that I needed it my brain didn't add 2+2 together to take me back to the video so I had to rediscover it. At least, the video is so good that rediscovering it doesn't feel bad at all.

First of all, I want to point out an error I committed in the original post.

Let's say we are adding two numbers. The result is simple.
$$2+3=5$$
However, let's now think of a scenario where 2 and 3 are not set. Instead, they follow a probability distribution. To start with something simple, let's assume they are constant distributions as shown.
View attachment 341883

In this case, I believe that's right so I know how to do it.
$$(2\pm 0.5)+(3\pm 1)=5\pm 1.5$$

The result I posted is not the correct probability density function. The whole spectrum of possibilities is indeed right. The result will vary between $3.5$ and $6.5$. However, the probabilities assigned in the drawing are not correct.
To find the correct probability distribution it is necessary to apply the convolution to the two original probability density functions.

NOTE: The functions for the dice are weird because he's talking about weighted dice in that case.

I initially proposed those constant probability functions because they seemed like the simplest possible option but it turns out that, since the functions are defined in segments and there is no variable in those segments, the convolution formula isn't as straightforward.
I generalized it using two step functions so the probability distributions are defined by just one function in all $\mathbb{R}$.

Once that's done, it is easy to apply the formulas as long as it is a computer crunching the numbers.
I created a little demo in Desmos in which you can play around with the numbers to see how it changes things. Just be wary to keep $a<b$, $c<d$ and $k$ not too big because I feel it overflows the calculator.
https://www.desmos.com/calculator/4swxqgoh6d
NOTE: I checked all areas under the probability density functions and the result is 1. Although the resultant probability density function from the convolution is not plotted, I checked it as well.
I couldn't plot the resultant probability density function in Desmos but you can see how the function would evaluate for each $s$ using the slider for that variable. That also moves the graphs around. That is analogous to what the video shows at around 15:32. The final step is to integrate that probability density function between the two values you are interested in and you'll obtain the probability of the sum being within that interval.

So, after all this, I feel capable of solving the problem in the forward direction as mentioned in the OP.

Given the number $a$ with this probability distribution (whichever) and the number $b$ with this probability distribution (whichever), what is the probability that the sum c falls within the numbers $e$ and $d$.

The inverse problem is yet to be solved.

Similarly, the following question would be interesting to answer:

Given the target of the number $c$ being within the limits caused by $e$ and $d$ with a 95% certainty, how should $a$ and $b$ be given that they follow this probability distribution (whichever)?
This second question would look a lot like what a designer would need to face when choosing the tolerances of machined parts. The first one allows us to check if what was chosen is right. The second one is like trying to find the best answer directly.
I am aware that the second question has infinite solutions because the problem is not sufficiently defined. I don't know how to restrain it a little more so it is still realistic and will spit out the best possible solution directly. I would guess an additional restraint would be to force the tolerance brackets to be as big as possible in both numbers so the parts are easier to manufacture. "Big" is relative, so I would define big as a percentage of the average.

I have already gone numerical so I am not expecting an analytical pretty solution but I guess I'm OK with that. I'm thinking of calculating a bunch of combinations defining the boundaries of the two initial numbers and then choosing the combination that results in the intervals being the biggest while still fulfilling the condition. It would be like solving the forward problem several times changing things and then choosing the best option from them all.
I am aware I am not following a very efficient calculation method but, at this level, I will choose clarity and computer power over other parameters.

Lastly, any input regarding the possible probability density distributions to be expected in parts from workshops?

As a last bonus question, I mentioned at the top of the post that the applicability of this is limited by the actual knowledge of the probability distributions present in machined parts. Let's imagine I ask for 100 cylinders to be machined to 50±0.5 mm in diameter. I believe the machinist will keep removing material with his lathe until he's within the tolerance bracket. He has no particular interest in giving me the part being as close to the nominal value as possible since that risks scrapping a part because he removed more material than necessary. Therefore, my current guess is that the distributions must look somewhat like this:
View attachment 341886
That is only an educated guess in which even psychology is involved. The machinist might be somewhat of a perfectionist and he wants to get close to the average value. The only way to know would be to take all manufactured parts and get the probability distribution but that implies the job is already done so you cannot modify the tolerance bracket in the design to nail the target you initially had in mind. Is there a best way to approach this? What probability distribution would you apply?

So far, all my work is in low volumes so even if I knew the details of this problem there is little chance they would be representative enough to apply it but I still think it's an interesting matter to think about and it might be more useful in the future. Knowledge is power.

Let me know your thoughts.
Thanks in advance.

 

[FactChecker]

The way to handle this is a little harder than your first idea of just adding the $\pm$ numbers but is much simpler than your latest post. You do not need to know the entire probability distribution and compute convolutions.

When you say that one variable, X, is $2 \pm 0.5$, you are saying that you have some level of confidence that the value will be within $\pm 0.5$ of $2$. Assume that you are using the same level of confidence for the second variable, Y, and can say with that confidence that it is within $\pm 1$ of $3$. Also assume that the variation of the two variables, X and Y, are independent of each other.
Suppose that you want to keep the same level of confidence for the sum, X+Y, being within some distance of the mean of X+Y. The trick is that to find the deviation of the sum, you must add the squares of the individual deviations and then take the square root. So you should calculate $\sqrt {0.5^2 + 1^2} = \sqrt {1.25} = 1.118$. The final answer is $5 \pm 1.118$ with the same confidence of the original two variables.

EDIT, ADDED JUSTIFICATION: Let $\mu_X$ and $\mu_Y$ denote the means of the variables and $\sigma_X, \sigma_Y$ their standard deviations. Saying that you want the same level of confidence that the variables, X, Y, and X+Y to be within a certain distance of their means is to say that you want the $\pm$ numbers to be the same multiple, a, of their respective standard deviations. That is, you want $a\cdot\sigma_X, a\cdot\sigma_Y, a\cdot\sigma_{X+Y}$ to be 0.5, 1, and [to be determined].
The equation for $a\cdot\sigma_{X+Y}$ is $a \sqrt{ \sigma_X^2 + \sigma_Y^2} = \sqrt{(a\cdot\sigma_X)^2 + (a\cdot\sigma_Y)^2} = \sqrt {0.5^2 + 1^2} = \sqrt {1.25} = 1.118$

EDIT, ADDED INTUITION ON WHY THE TOLERANCES SHOULD NOT JUST BE ADDED:
Consider an extreme case where one variable, X, has a relatively huge uncertainty (like 1000) and the other, Y, has a very small uncertainty (like 0.1). Then the question is whether the uncertainty of the sum X+Y would be 1000.1. The answer is no. The small uncertainty of Y is not likely to push the sum out of the tolerance of X except for the small fraction of the time that X is within [-1000.1,-999.9] or [+999.9, 1000.1]. So most of the time, the uncertainty of Y does not matter. It has very little effect on the X+Y region of the confidence level -- much smaller than 0.1.

 

[Juanda]

When you say that one variable, X, is $2 \pm 0.5$, you are saying that you have some level of confidence that the value will be within $\pm 0.5$ of $2$. Assume that you are using the same level of confidence for the second variable, Y, and can say with that confidence that it is within $\pm 1$ of $3$. Also assume that the variation of the two variables, X and Y, are independent of each other.
Suppose that you want to keep the same level of confidence for the sum, X+Y, being within some distance of the mean of X+Y. The trick is that to find the deviation of the sum, you must add the squares of the individual deviations and then take the square root. So you should calculate $\sqrt {0.5^2 + 1^2} = \sqrt {1.25} = 1.118$. The final answer is $5 \pm 1.118$ with the same confidence of the original two variables.

What do you mean by "you have some level of confidence that the value will be within $\pm 0.5$ of $2$"?
I believe we're misunderstanding each other because you're assuming a normal distribution for the pdf. I think you're assuming that because you're talking about standard deviation and confidence. I was talking about a general case and did this example with a constant distribution because I thought it'd be the simplest although I was proven wrong as exposed in post #4.

I initially proposed those constant probability functions because they seemed like the simplest possible option but it turns out that, since the functions are defined in segments and there is no variable in those segments, the convolution formula isn't as straightforward.

If I try to apply your logic to this constant distribution I get strange results. In that example, I assumed a constant pdf so I have 100% confidence the number will be within those margins.
Following the logic you exposed, does that mean that I can be 100% confident that the sum will be $5 \pm 1.118$? That makes no sense to me.
I cannot draw the exact resultant pdf from the convolution yet. But looking at how the value that the resultant pdf would take changes as I use the slider that defines $s$ I can see it'd look like a trapezoid.

By the way, that result coincides with the intuition you mentioned in your second edit. It's less likely to obtain a very small sum because it'd require both inputs to be very small. The same applies to a big sum. It's the numbers in the middle that will be more likely because they can be produced by:

1. Medium number + Medium number
2. Big number + Small number
3. Small number + Big number

 

[FactChecker]

I guess we are talking about different things. IMO, the logic in my posts apply to general random variables that have a finite mean and standard deviation. I don't see right now what breaks down in my logic for your 100% confidence example.
Regardless of the probability distribution, doesn't your logic for 100% confidence always work? I don't see anything else that needs to be done and I agree with your original post in that situation. The only complication would be if the two random variables are related in a way that might always force some cancellations of the extreme deviations.

 

[Juanda]

Regardless of the probability distribution, doesn't your logic for 100% confidence always work?

I am pretty sure the method I exposed works for any pdf.

I don't see anything else that needs to be done and I agree with your original post in that situation. The only complication would be if the two random variables are related in a way that might always force some cancellations of the extreme deviations.

Dependent variables are out of the question. Still, I disagree. I think there is still depth to explore. More concretely applied to this case, the two points left in the OP and reiterated in post #4.

1. Solving the inverse problem.
2. Finding the connection to the real world to assess the correct pdf to the two original values that will be summed.

To solve the inverse problem I proposed this method although I am curious to know if there is a better alternative.

The inverse problem is yet to be solved.

I have already gone numerical so I am not expecting an analytical pretty solution but I guess I'm OK with that. I'm thinking of calculating a bunch of combinations defining the boundaries of the two initial numbers and then choosing the combination that results in the intervals being the biggest while still fulfilling the condition. It would be like solving the forward problem several times changing things and then choosing the best option from them all.
I am aware I am not following a very efficient calculation method but, at this level, I will choose clarity and computer power over other parameters.

To find the actual pdf of the two variables though... I don't really know if there is a way to know besides experimentally. Maybe someone with experience has already been in those shoes and can provide some insight.

As a last bonus question, I mentioned at the top of the post that the applicability of this is limited by the actual knowledge of the probability distributions present in machined parts. Let's imagine I ask for 100 cylinders to be machined to 50±0.5 mm in diameter. I believe the machinist will keep removing material with his lathe until he's within the tolerance bracket. He has no particular interest in giving me the part being as close to the nominal value as possible since that risks scrapping a part because he removed more material than necessary. Therefore, my current guess is that the distributions must look somewhat like this:
View attachment 341886
That is only an educated guess in which even psychology is involved. The machinist might be somewhat of a perfectionist and he wants to get close to the average value. The only way to know would be to take all manufactured parts and get the probability distribution but that implies the job is already done so you cannot modify the tolerance bracket in the design to nail the target you initially had in mind. Is there a best way to approach this? What probability distribution would you apply?

So far, all my work is in low volumes so even if I knew the details of this problem there is little chance they would be representative enough to apply it but I still think it's an interesting matter to think about and it might be more useful in the future. Knowledge is power.

Let me know your thoughts.
Thanks in advance.