Calculate Length Contraction for Accelerated Motion to Proxima Centauri

[ntrand]

TL;DR Summary

I want to calculate length contraction from Earth to Proxima Centauri in the reference frame of a spaceship that is moving with acceleration between those two points.

Let's assume a spaceship traveling from the Earth to the Proxima Centauri with constant acceleration g = 9.81 m/s².

The ship is accelerating the first half of the trajectory and decelerating the second half.

I calculated the velocity profile from the Earth reference:

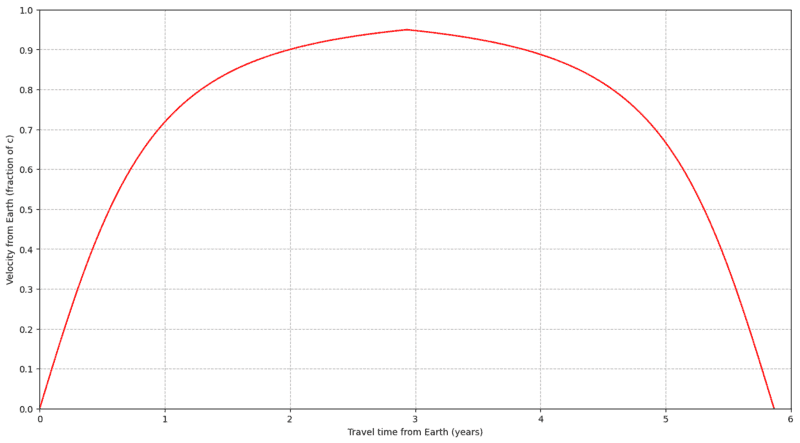
The travel time on the spaceship is calculated to be 3.54 years due to the time dilation.

In order to calculate the length contraction from Earth to Proxima Centauri, I started with the formula:

where l₀ is length from the Earth reference.

Then I insert the velocity formula:

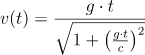
but I am not able to calculate the integral since the independent variable is length l instead of time t.

How can I calculate length contraction for such accelerated motion? I want to calculate the length from Earth to Proxima in the ship frame.

 

[Ibix]

Length contraction is a phenomenon defined for inertial frames only. Your frame is not inertial, and for non-inertial coordinates there isn't really a unique answer since it depends on which non-inertial coordinates you choose to use. Why do you want to know? That might help in choosing an approach.

 

[PeroK]

In order to calculate the length contraction from Earth to Proxima Centauri, I started with the formula:

View attachment 319392

where l₀ is length from the Earth reference.

Then I insert the velocity formula:

View attachment 319393

but I am not able to calculate the integral since the independent variable is length l instead of time t.

I fail to see the relevance or importance of this calculation. In any case, I wouldn't describe it as a calculation of length contraction.

 

[ntrand]

Length contraction is a phenomenon defined for inertial frames only. Your frame is not inertial, and for non-inertial coordinates there isn't really a unique answer since it depends on which non-inertial coordinates you choose to use. Why do you want to know? That might help in choosing an approach.

Let's stick with the trajectory of the spaceship (coordinates are onboard the ship during the whole trip).

 

[PeroK]

Let's stick with the trajectory of the spaceship (coordinates are onboard the ship during the whole trip).

Coordinates are not physical objects that you can keep onboard a ship!

 

[Ibix]

Let's stick with the trajectory of the spaceship (coordinates are onboard the ship during the whole travel time).

"Coordinates are onboard the ship" makes no sense, I'm afraid.

If you mean "how far does the ship travel in its own rest frame" the answer is zero. You need to ask how far Proxima travels, which depends on how you define your coordinates.

 

[ntrand]

"Coordinates are onboard the ship" makes no sense, I'm afraid.

If you mean "how far does the ship travel in its own rest frame" the answer is zero. You need to ask how far Proxima travels, which depends on how you define your coordinates.

I don't understand why coordinates (or rather coordinate's origin) onboard the ship doesn't make any sense.

Anyway, the purpose of this task is to explain the twin paradox. If you check wiki, the traveler's perspective takes into account the length contraction "between the Earth and the star system in their rest frame". I want to calculate the same for the accelerated motion above.

 

[Ibix]

I don't understand why coordinates (or rather coordinate's origin) onboard the ship doesn't make any sense.

Having the origin at the ship makes sense. But you still need to define coordinates that cover the whole journey, which is a lot more than just where the origin is.

Anyway, the purpose of this task is to explain the twin paradox. If you check wiki, the traveler's perspective takes into account the length contraction "between the Earth and the star system in their rest frame". I want to calculate the same for the accelerated motion above.

Don't do it that way, then, because the distance travelled isn't well defined. Just work out the time taken from the equations for constant proper acceleration.

 

[PeroK]

Anyway, the purpose of this task is to explain the twin paradox. If you check wiki, the traveler's perspective takes into account the length contraction "between the Earth and the star system in their rest frame". I want to calculate the same for the accelerated motion above.

The best answer to this is the one that @Ibix gave in post #2: that length contraction is essentially associated with measurements of length taken in an inertial reference frame. Length contraction doesn't really have a generalisation within SR to accelerating reference frames or more general coordinate systems.

 

[Ibix]

If you check wiki, the traveler's perspective takes into account the length contraction "between the Earth and the star system in their rest frame". I want to calculate the same for the accelerated motion above.

The "specific example" in the wiki you linked is terrible, and very difficult to generalise to accelerated motion because it makes a lot of simplifying assumptions that only work for inertial frames, and are littered with traps for the unwary. For example, naively applying the reasoning used there to calculate elapsed time for mission control from the "traveller's perspective" would lead you to exactly the paradox that mission control "ought to be" younger. It's missed the entire point of the scenario, which is to explain why that is incorrect.

 

[PeroK]

@ntrand a useful exercise is to calculate the proper time that elapses on the ship between Earth and Proxima with that acceleration profile.

There are then a number of ways of analysing the scenario from the ship's perspective. I'm not sure what would be the simplest. That said, proving that the spacetime interval is invariant under any coordinate transformation is a clean, if mathematically more sophisticated, approach.

 

[Dale]

I don't understand why coordinates (or rather coordinate's origin) onboard the ship doesn't make any sense.

One issue is a matter of definition. For an inertial object, the object’s frame is well defined. There is an unambiguous standard meaning when someone says “the object’s frame”.

But for a non-inertial object there is no such well defined meaning. In order to say “the object’s frame” for a non-inertial object you have to also describe the mathematical or physical process that you wish to use for constructing such a frame.

There are many possibilities in the literature. My favorite is radar coordinates. The frame is constructed by sending and receiving radar pulses from the object to each event. In units where c=1 the time of the event is halfway between the send and receive time and the distance is half of the difference between the send and receive times.

 

[PeterDonis]

the purpose of this task is to explain the twin paradox

The twin paradox is about different elapsed proper times for two twins that separate and then meet up again. There are no such twins in your scenario.

Also, the twin paradox is about times, not lengths. I'm not clear how any calculation of length contraction would help to explain the difference in times.

 

[ntrand]

@ntrand a useful exercise is to calculate the proper time that elapses on the ship between Earth and Proxima with that acceleration profile.

There are then a number of ways of analysing the scenario from the ship's perspective. I'm not sure what would be the simplest. That said, proving that the spacetime interval is invariant under any coordinate transformation is a clean, if mathematically more sophisticated, approach.

I am able to calculate:
a) time elapsed on the ship is 3.54 years
b) spacetime interval of the trip is 33483585728808616 m

How can I prove within SR that time elapsed on Earth is still 5.87 years when reversing the logic and considering that Earth accelerates away from the ship?

 

[Ibix]

How can I prove within SR that time elapsed on Earth is still 5.87 years when reversing the logic and considering that Earth accelerates away from the ship?

Easy way: note that proper time is manifestly invariant. Job done.

Hard way: set up a coordinate system where your ship is at rest (Rindler or radar coordinates will do), express the Earth's worldline in these coordinates, and integrate its proper time.

 

[PeroK]

How can I prove within SR that time elapsed on Earth is still 5.87 years when reversing the logic and considering that Earth accelerates away from the ship?

I agree with what @Ibix said. I have looked at something similar, which is a clock continuously orbiting a "stationary" (i.e. inertial clock). In this case, velocity-based time dilation itself is symmetric; and yet, there must be differential aging between the orbiting (accelerating clock). I did this by breaking down the orbit into a series of discrete, instantaneous changes of direction and using the usual inertial motion calculations for each stage. You can find that here:

https://www.physicsforums.com/threa...ther-in-a-circular-orbit.896607/#post-5660815

 

[Ibix]

b) spacetime interval of the trip is 33483585728808616 m

Also, if you have an elapsed time of 3.54 years there is no way you can justify that many significant figures. You do not know your trip time accurate to a nanosecond or two.

 

[Dale]

How can I prove within SR that time elapsed on Earth is still 5.87 years when reversing the logic and considering that Earth accelerates away from the ship?

You can use the radar approach I mentioned earlier and then use this paper to calculate the metric in the non-inertial frame:

https://arxiv.org/abs/physics/0412024

 

[Sagittarius A-Star]

I am able to calculate:
a) time elapsed on the ship is 3.54 years
...
How can I prove within SR that time elapsed on Earth is still 5.87 years when reversing the logic and considering that Earth accelerates away from the ship?

These numbers are correct. I checked them against my calculation for the case $\alpha = c = 1$ by inserting your $\alpha / c$ instead of my $\alpha =1$ and checked with $t_2 = 3.54 years /2$ and $T_2 = 5.87 years / 2$.

Source:
https://www.physicsforums.com/threads/twin-paradox-with-accelerated-motion.1047089/

Also, I did a plausibility check of my calculation in the inertial frame with a calculation in the accelerated Rinder frame.

Source:
https://www.physicsforums.com/threads/twin-paradox-with-accelerated-motion.1047089/post-6819344

 

[Sagittarius A-Star]

How can I prove within SR that time elapsed on Earth is still 5.87 years when reversing the logic and considering that Earth accelerates away from the ship?

Hard way: set up a coordinate system where your ship is at rest (Rindler or radar coordinates will do), express the Earth's worldline in these coordinates, and integrate its proper time.

I will use Rindler-coordinates ($ct, x$) for the accelerated frame of Bob, who is at rest at $x=\frac{c^2}{\alpha}$ and has the proper acceleration $\alpha = 9.81 m/s^2$. The Rindler transformation is:

$cT = x \sinh(\frac{\alpha}{c^2} ct) \ \ \ \ \ (1)$
$X = x \cosh(\frac{\alpha}{c^2} ct) \ \ \ \ \ (2)$

The time-dilation formula in Bob's rest-frame follows from the metric in Rindler-coordinates:
$$d\tau = dt \sqrt{(\frac{\alpha x}{c^2})^2-\frac{v^2}{c^2}}\ \ \ \ \ (3)$$Source:
https://en.wikipedia.org/wiki/Rindler_coordinates#math_1a

Bob's time-dilation factor is $1$, because he is at rest ($v=0$) at $x=\frac{c^2}{\alpha}$, see equation (3).
To calculate Alice's time-dilation with reference to Bob's accelerated rest-frame, I need to derive her $x(t)$ and $v(t)$.

With above equation (2) and $L =$ proper distance between Earth and Proxima Centauri follows for Alice:
$\require{color} \color{red} x(t) \color{black} = (L+\frac{c^2}{\alpha}) / \cosh(\frac{\alpha}{c^2} ct) \ \ \ \ \ (4)$
$\require{color} v(t) = dx/dt = (L+\frac{c^2}{\alpha}) (-\frac{\alpha}{c^2} c) (\tanh(\frac{\alpha}{c^2} ct) / \cosh(\frac{\alpha}{c^2} ct)) = - c \tanh(\frac{\alpha}{c^2} ct) \frac{\alpha}{c^2} \color{red}x(t) \color{black} \ \ \ \ \ (5)$

Calculation:
https://www.wolframalpha.com/input?i2d=true&i=D[Divide[1,cosh\(40)at\(41)],t]

In equation (5), $v(t)$ is minus Bob's velocity in Alice's frame, multiplied by $\frac{\alpha}{c^2}x(t)$. This indicates, that Alice's velocity in Bob's frame is influenced by the "gravitational" time-dilation in the accelerated reference frame.

Source:
https://en.wikipedia.org/wiki/Hyperbolic_motion_(relativity)#Worldline

Plugging equations (4) and (5) for Alice into above time-dilation formula (3):

$d\tau = dt (L+\frac{c^2}{\alpha}) \sqrt{(\frac{\alpha}{c^2}/ \cosh(\frac{\alpha}{c^2} ct))^2(1-\tanh^2(\frac{\alpha}{c^2} ct))}$​

$= dt (\frac{L\alpha}{c^2}+1) \sqrt{\cosh^{-2}(\frac{\alpha}{c^2} ct)\cosh^{-2}(\frac{\alpha}{c^2} ct)}$​

$= dt (\frac{L\alpha}{c^2}+1) \cosh^{-2}(\frac{\alpha}{c^2} ct)$​

Integrating this, to get the time-coordinate of event $E_2$ in Alice's frame:

$T_2=(\frac{L\alpha}{c^2}+1) \int_0^{t_2} \cosh^{-2}(\frac{\alpha}{c^2} ct)\ dt$​

$=(\frac{L\alpha}{c^2}+1) \frac{c}{\alpha}\tanh(\frac{\alpha}{c^2} ct_2) \require{color} =(L+\frac{c^2}{\alpha}) \frac{1}{c} \frac{\sinh(\alpha t_2/c)}{\cosh(\alpha t_2/c)} = \frac{\color{red}x(t_2)\color{black}}{c} \sinh(\frac{\alpha}{c^2} ct_2)$​

$= \frac{c}{\alpha} \sinh(\frac{\alpha}{c^2} ct_2)$​

Calculation:
https://www.wolframalpha.com/input?i2d=true&i=Integrate[Divide[1,Power[cosh,2]\(40)at\(41)],t]

I take for event $E_2$ your $t_2 = 3.54 years /2$ into equation
$T_2= \frac{c}{\alpha} \sinh(\frac{\alpha}{c^2} ct_2)$.
Then I get $T_2 = 5.87 years /2$.

Edit, after discussion with @Ibix : This posting describes another scenario than the OP. I overlooked, that the diagram in the OP is a velocity / time diagram instead of a spacetime diagram.

 

[Ibix]

$\DeclareMathOperator{\sinh}{sinh}\DeclareMathOperator{\sech}{sech}$I thought I would work this out.

Let's call the distance from Earth to Proxima $L$, and say the rocket accelerates at constant proper acceleration $\alpha$. Given a set of inertial coordinates $T,X$ we can define a set of Rindler coordinates $t,x$, and we have transforms $$\begin{eqnarray*}
T&=&x\sinh(\alpha t)\\
X&=&x\cosh(\alpha t)\\
x&=&\sqrt{X^2-T^2}\tag{1}\\
t&=&\frac 1\alpha\tanh^{-1}\left(\frac TX\right)\tag{2}
\end{eqnarray*}$$and a line element$$ds^2=(\alpha x)^2dt^2-dx^2$$(Ref) First, we need to write down the trajectory of the Earth in these coordinates. In the inertial cordinates the Earth is at some fixed $X$, say $X=D$, for all $T$. We can plug this into (1) and (2) and eliminate $T$ to get (edit: after minor typo correction from @Sagittarius A-Star )$$\begin{eqnarray*}
x&=&D\sech(\alpha t)\tag{3}\\
\frac{dx}{dt}&=&-\alpha D\sech(\alpha t)\tanh(\alpha t)\tag{4}
\end{eqnarray*}$$We can then use these with the line element to get the $ds^2$ for Earth between Rindler times $t$ and $t+dt$.$$\begin{eqnarray*}
ds^2&=&(\alpha x)^2dt^2-dx^2\\
&=&\left((\alpha x)^2-\left(\frac{dx}{dt}\right)^2\right)dt^2\\
&=&\alpha^2D^2\sech^4(\alpha t)dt^2
\end{eqnarray*}$$where we used (3) and (4) and simplified to get from the second line to the third. We can then just take the square root and integrate to get the Earth's proper time between two Rindler coordinate times, $t_i$ and $t_f$:$$\begin{eqnarray*}
\tau&=&\int_{t=t_i}^{t_f}ds\\
&=&\alpha D\int_{t_i}^{t_f}\sech^2(\alpha t)dt\\
&=&D\left(\tanh(\alpha t_f)-\tanh(\alpha t_i)\right)\tag{5}
\end{eqnarray*}$$Finally, we need to know the $t$ coordinate when our rocket turns over and begins to decelerate. We can use the fact that turnover happens in the inertial frame at $L/2$ from the Earth, and that the Earth's $X$ coordinate is $1/\alpha$ to write the "half way" $X$ coordinate $X_{1/2}=1/\alpha+L/2$, or $X_{1/2}=(2+\alpha L)/2\alpha$. We know that the rocket has a constant $x=1/\alpha$. Thus we can use (1) and (2) to write the "half way" $T$ and $t$ coordinates also:$$\begin{eqnarray*}
X_{1/2}&=&\frac{2+\alpha L}{2\alpha}\\
T_{1/2}&=&\sqrt{\frac L{4\alpha}(\alpha L+4)}\\
t_{1/2}&=&\frac 1\alpha\tanh^{-1}\left(\frac{T_{1/2}}{X_{1/2}} \right)
\end{eqnarray*}$$We now have all the pieces we need to solve this problem. We will define two Rindler coordinate systems.

The first Rindler system covers the acceleration phase. Its origin is $1/\alpha$ to the left of Earth and its $t=0$ line runs through the departure event. The Earth is "below" the rocket with $D=D_1=1/\alpha$, and we use this coordinate system from $t=0$ to $t=t_{1/2}$. Plugging this into (5) we find that during the acceleration phase the Earth experiences proper time $\tau_1=D_1T_{1/2}/X_{1/2}$. Meanwhile, the rocket experienced proper time $t_{1/2}$ since its proper time matches coordinate time.

The second Rindler system covers the deceleration phase. Its origin is $1/\alpha$ to the right of Proxima and its $x$ coordinate increases to the left. Its $t=0$ line runs through the arrival event, and (by symmetry) we use it from $t=-t_{1/2}$ to $t=0$. In this system the Earth is "above" the rocket and has $D=D_2=1/\alpha+L$. Again we can plug all this into (5) and find that the Earth experiences proper time $\tau_2=D_2T_{1/2}/X_{1/2}$. Again, the rocket experienced $t_{1/2}$.

Noting that Proxima Centauri is $L=4.2465\mathrm{ly}$ from Earth (ref) and we want our rocket to accelerate at $\alpha=1\mathrm{g}=1.032\mathrm{ly/y^2}$, and putting everything together$$\begin{eqnarray*}
\tau_{\mathrm{Earth}}&=&\tau_1+\tau_2\\
&=&\sqrt{\frac L\alpha(\alpha L+4)}\\
&=&5.87\mathrm{y}\\
\tau_{\mathrm{rocket}}&=&2t_{1/2}\\
&=&\frac 2\alpha\tanh^{-1}\left(\frac{\sqrt{\alpha L(\alpha L+4)}}{\alpha L+2}\right)\\
&=&3.54\mathrm{y}
\end{eqnarray*}$$This matches the OP’s calculation.

 

[ntrand]

Thank you for detailed calculation!

I can also share my calculation in the non-inertial reference frame of the ship. I used Rindler coordinates and just integrated them along the trip.

First I calculated traveled distance and got the exact same number as observed from the Earth:
$$dx = c\cdot \sinh\left( \frac{\alpha}{c}\cdot t_0 \right)\cdot dt_0$$
$$x = 2\cdot \int_0^{1.77\ y} c\cdot \sinh\left(\frac{\alpha}{c}t_0\right)\ dt_0 = 4.24\ LY$$

The flight time passed on the Earth resulted in the same value compared to the inertial frame:
$$dt = \cosh\left( \frac{\alpha}{c}\cdot t_0 \right)\cdot dt_0$$
$$t = 2\cdot \int_0^{1.77\ y} \cosh\left(\frac{\alpha}{c}t_0\right)\ dt_0 = 5.87\ years$$

These calculations lead me to two considerations:
1) I wasn't able to calculate any length contraction between the Earth and Proxima. I am not sure how the "length contraction" is manifested in this situation.
2) Less time elapses on the ship during the flight compared to the Earth. That is interesting since both systems seems fairly equivalent. How does it come that less time passes on the ship and not on the Earth? The only physical difference I can see is the non-inertial nature of the spaceship. Does it mean that kinetic time dilation manifests more in the non-inertial systems? I am not clear on this.

 

[PeroK]

1) I wasn't able to calculate any length contraction between the Earth and Proxima. I am not sure how the "length contraction" is manifested in this situation.

As was mentioned previously, "length contraction" is a specific effect when comparing lengths in two inertial frames. More generally, length contraction isn't a "thing" in relativity.

2) Less time elapses on the ship during the flight compared to the Earth. That is interesting since both systems seems fairly equivalent. How does it come that less time passes on the ship and not on the Earth? The only physical difference I can see is the non-inertial nature of the spaceship. Does it mean that kinetic time dilation manifests more in the non-inertial systems? I am not clear on this.

Assuming this is a one-way trip, you are not comparing two physically equivalent quantities. You have calculated the coordinate time between two events in the IRF in which the Earth is at rest. And, you have calculated the proper time of the ship between those two events.

 

[Orodruin]

1) I wasn't able to calculate any length contraction between the Earth and Proxima. I am not sure how the "length contraction" is manifested in this situation.

Just to add to the post above: Although taught extensively in introductory relativity courses, length contraction and time dilation are not as fundamental as those courses would have you believe. Instead, they both rest upon particular formulations of setups — including inertial frames and the corresponding relativity of simultaneity. Length contraction as such is simply not directly applicable to general coordinate frames. There are ways of generalising the concept, but it then becomes even more coordinate dependent and ultimately not a very useful tool.

 

[Ibix]

2) Less time elapses on the ship during the flight compared to the Earth.

There's an unexamined assumption here (and in my work) that we use the Earth's inertial simultaneity convention to judge "when" the Earth says the rocket has arrived at Proxima. You can avoid this assumption by having the rocket return to Earth, as Peter alluded earlier.

Then the result is easy to understand. The elapsed time is $\int ds$, and $ds$ is the non-Euclidean generalisation of the elementary distance along a line. So the elapsed time is the "length" of the worldline. And the rocket and the Earth followed different paths, so it shouldn't surprise you that the lengths are different. The only thing to add is that (for timelike paths) the straight line is the longest distance between two points. So the inertial observer is always the oldest.

Note that I haven't mentioned frames or time dilation at all. They are heavily emphasised in introductory relativity, as Orodruin says, but far less useful and more confusing as one goes to more complex scenarios.

 

[Sagittarius A-Star]

$\DeclareMathOperator{\sinh}{sinh}\DeclareMathOperator{\sech}{sech}$$$\begin{eqnarray*}
X&=&x\cosh(\alpha t)\\
\end{eqnarray*}$$

I think, there is a square too much at the $\sech$ function in equation (3), compare to above Rindler transformation.

$$\begin{eqnarray*}
x&=&D\sech^2(\alpha t)\tag{3}
\end{eqnarray*}$$

 

[Ibix]

I think, there is a square too much at the $\sech$ function in equation (3), compare to above Rindler transformation.

Indeed - and it had carried through to the next line too. Corrected above, thanks.

 

[Sagittarius A-Star]

$\DeclareMathOperator{\sinh}{sinh}\DeclareMathOperator{\sech}{sech}$Finally, we need to know the $t$ coordinate when our rocket turns over and begins to decelerate. We can use the fact that turnover happens in the inertial frame at $L/2$ from the Earth, and that the Earth's $X$ coordinate is $1/\alpha$ to write the "half way" $X$ coordinate $X_{1/2}=1/\alpha+L/2$, or $X_{1/2}=(2+\alpha L)/2\alpha$. We know that the rocket has a constant $x=1/\alpha$. Thus we can use (1) and (2) to write the "half way" $T$ and $t$ coordinates also:$$\begin{eqnarray*}
X_{1/2}&=&\frac{2+\alpha L}{2\alpha}\\
T_{1/2}&=&\sqrt{\frac L{4\alpha}(\alpha L+4)}\\
t_{1/2}&=&\frac 1\alpha\tanh^{-1}\left(\frac{T_{1/2}}{X_{1/2}} \right)
\end{eqnarray*}$$We now have all the pieces we need to solve this problem. We will define two Rindler coordinate systems.
The first Rindler system covers the acceleration phase.

According to my understanding of the velocity profile in the OP, the rocket accelerates between the two meeting events of the twins only towards the earth. Then only one Rinder frame is needed.

 

[Ibix]

According to my understanding of the velocity profile in the OP, the rocket accelerates between the two meeting events of the twins only towards the earth. Then only one Rinder frame is needed.

I disagree - the velocity is initially zero, rises to a maximum, then falls back to zero. The acceleration is also discontinuous at the middle. This is a one-way trip with a turnover in the middle.

The total time is the same as various other scenarios where $|\alpha|$ is constant, yes.

 

[Sagittarius A-Star]

I disagree - the velocity is initially zero, rises to a maximum, then falls back to zero. The acceleration is also discontinuous at the middle. This is a one-way trip with a turnover in the middle.

You are correct. I overlooked, that the diagram in the OP is a velocity / time diagram instead of a spacetime diagram.