Aja
- 4
- 0
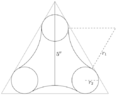
A sad and strange image, I know, but better than none at all. What you see is a stake I'm trying to model using CAD software. With the dimension given (5 inches--in case it's not clear, the distance from the top of the equilateral triangle that encloses this shape to the midpoint of the red arc) I'm willing to bet that I can calculate the length of that arc or other dimensions that will help me model this accurately.
Any ideas?
https://www.physicsforums.com/attachments/4116
Any ideas?
https://www.physicsforums.com/attachments/4116