Can someone please explain Feynman's index notation?

[etotheipi]

I found some parts of Vol II, Chapter 25 basically unreadable, because I can't figure out his notation. AFAICT he's using a (+,-,-,-) metric, but these equations don't really make any sense:

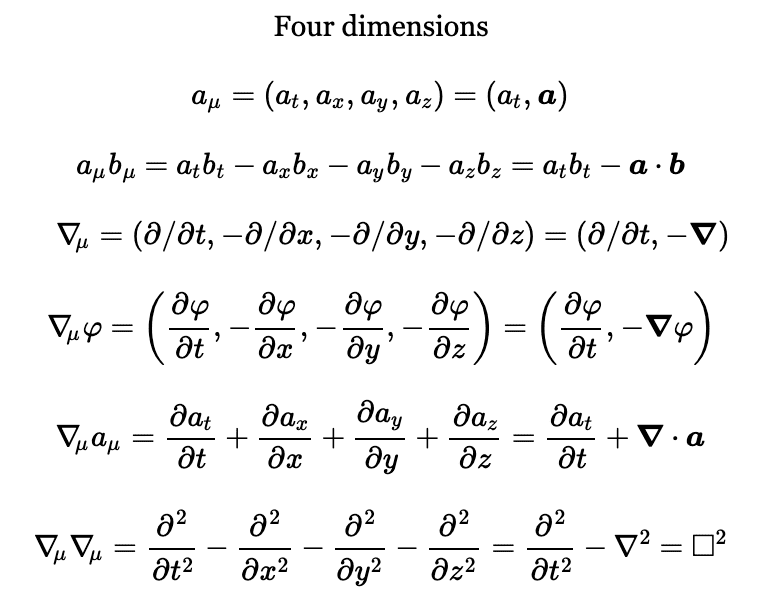
The first one is fine, and so is the second so long as we switch out $a_{\mu} b_{\mu}$ for $a_{\mu} b^{\mu}$. But I'm pretty certain the second one should be$$\nabla_{\mu} = (\partial_t, \partial_x, \partial_y, \partial_z) = (\partial_t, \nabla)$$whilst the fifth should be$$\nabla_{\mu} a^{\mu} = \partial_t a^t + \partial_x a^x + \partial_y a^y + \partial_z a^z = \partial_t a_t - \partial_x a_x - \partial_y a_y - \partial_z a_z = \partial_t a_t - \nabla \cdot \mathbf{a}$$and finally the sixth is okay, but again only so long as we switch out $\nabla_{\mu} \nabla_{\mu}$ for $\nabla_{\mu} \nabla^{\mu}$.

One might argue that he's put everything downstairs to avoid confusion (!), but given that index placement is of such importance when we have a metric that is not the identity, I wonder if there's a subtlety to his notation that I missed? Thank you.

 

[Ibix]

He's not using the metric explicitly, but making it implicit in his expressions. So he can use all-lower indices because he doesn't use raising and lowering explicitly. Note that his expressions for inner products and the gradient operator work out the same as more standard notation in component terms, but only because he's put the signs in by hand.

I don't think I've read Feynman's take on relativity, certainly not in a long time, but if memory serves @vanhees71 always comments that the mathematical presentation is one of the few bits where he think Feynman mis-stepped.

 

[fresh_42]

What is $\partial_t$ if not $\dfrac{\partial}{\partial t}$?

The german Wiki page about Einstein notation notes both versions: $a_\mu b_\mu=a_\mu b^\mu$:
https://de.wikipedia.org/wiki/Einsteinsche_Summenkonvention
as with and without index position.

I think it makes perfectly sense.

 

[etotheipi]

@fresh_42 but the objects $\partial_{\mu} = \frac{\partial}{\partial x^{\mu}}$ and $\partial^{\mu} = \frac{\partial}{\partial x_{\mu}}$ are different. And also, I believe repeated indices should be summed over one upstairs and one downstairs, so $a_{\mu} b^{\mu}$ is valid, whilst $a_{\mu} b_{\mu}$ isn't.

 

[Gaussian97]

Well, certainly this is not Einstein notation so, how is the notation defined? What it means to have repeated indexes, etc...

If these equations are supposed to be definitions, there's nothing you can do about it, and they seem to perfectly coherent.

 

[etotheipi]

Right, thanks! So, in this context, do all the $a_{\mu}$ refer to contravariant components?

 

[Ibix]

I think it doesn't make a difference whether you think of them as contravariant or covariant, and Feynman isn't distinguishing. He'd only need to distinguish if he were making his metric explicit.

What I don't like is how $a_\mu b_\mu$ and $\nabla_\mu a_\mu$ work differently. In one case the minus signs seem to be part of the operator while in the other they seem to be part of the operation.

 

[fresh_42]

@fresh_42 but the objects $\partial_{\mu} = \frac{\partial}{\partial x^{\mu}}$ and $\partial^{\mu} = \frac{\partial}{\partial x_{\mu}}$ are different. And also, I believe repeated indices should be summed over one upstairs and one downstairs, so $a_{\mu} b^{\mu}$ is valid, whilst $a_{\mu} b_{\mu}$ isn't.

As I said, both is possible. It is an abbreviation and convention anyway, nothing written in stone. Look at the link I gave: they mention both notations. As long as there is only one summation, confusion can be excluded. It becomes important with multiple indices, not with one. The more as it is explained in the first line.

 

[etotheipi]

What I don't like is how $a_\mu b_\mu$ and $\nabla_\mu a_\mu$ work differently. In one case the minus signs seem to be part of the operator while in the other they seem to be part of the operation.

I think what he's going for, is something like$$\begin{align*}\nabla_{\mu} a_{\mu} &= \left(\frac{\partial}{\partial t} a_t \right) - \left(-\frac{\partial}{\partial x} a_x \right) - \left(-\frac{\partial}{\partial y} a_y \right) - \left(-\frac{\partial}{\partial z} a_z \right) \\

&= \frac{\partial a_t}{\partial t} + \frac{\partial a_x}{\partial x} + \frac{\partial a_y}{\partial y} + \frac{\partial a_z}{\partial z}\end{align*}$$I don't like the notation anyway, so I think I'll try to forget about it

 

[fresh_42]

I think what he's going for, is something like$$\begin{align*}\nabla_{\mu} a_{\mu} &= \left(\frac{\partial}{\partial t} a_t \right) - \left(-\frac{\partial}{\partial x} a_x \right) - \left(-\frac{\partial}{\partial y} a_y \right) - \left(-\frac{\partial}{\partial z} a_z \right) \\

&= \frac{\partial a_t}{\partial t} + \frac{\partial a_x}{\partial x} + \frac{\partial a_y}{\partial y} + \frac{\partial a_z}{\partial z}\end{align*}$$I don't like the notation anyway, so I think I'll try to forget about it

I wouldn't do that. It might mean that you cannot read a couple of books. Indices are very important in physics, but you cannot determine how different authors use(d) them.

 

[etotheipi]

I wouldn't do that. It might mean that you cannot read a couple of books. Indices are very important in physics, but you cannot determine how different authors use(d) them.

Perhaps, but I think the Einstein summation convention with proper index placement and whatnot is so prevalent nowadays that it's not worth stressing about this more obscure (and probably less versatile) notation.

 

[fresh_42]

Perhaps, but I think the Einstein summation convention with proper index placement and whatnot is so prevalent nowadays that it's not worth stressing about this more obscure (and probably less versatile) notation.

Well, Einstein was of different opinion than you. He used both.

Here is the original from 1918:

"For this we introduce the rule: If an index occurs twice in a term of an expression, it must always be summed up, unless the opposite is expressly noted.
...
Following Ricci and Levi-Civita, the contravariant character is indicated by the upper and the covariant by the lower index."

Since co- and contravariance is only determined by its transformation rules, there is no way to decide whether your equations above refer to either of them. As written, they are simply vectors, neither co- nor contravariant.

 

[vanhees71]

I don't think I've read Feynman's take on relativity, certainly not in a long time, but if memory serves @vanhees71 always comments that the mathematical presentation is one of the few bits where he think Feynman mis-stepped.

Yes, that's a nuissance. I don't understand, why Feynman is doing this. The only other thing which is really wrong in his famous lectures (as far as I'm aware of) is the relativistic treatment of the DC conducting wire, but that's done wrong in almost all textbooks I know of. See

https://www.physicsforums.com/insights/relativistic-treatment-of-the-dc-conducting-straight-wire/

and the AJP paper by Peters quoted therein.