Can the trace be expressed in terms of the determinant?

[Jhenrique]

Browsing in the wiki, I found those formulas:

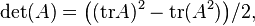
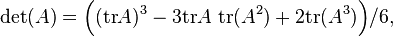
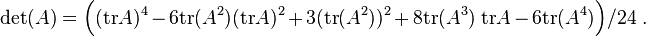
http://en.wikipedia.org/wiki/Determinant#Relation_to_eigenvalues_and_trace

So, my doubt is: if is possible to express the determinant in terms of the trace, thus is possible to express the trace in terms of the determinant too?

 

[fresh_42]

I don't think so. We can write $a_1\ldots a_n$ in terms of weighted sums of $(a_1+\ldots +a_n)^k$ but I don't think the other way around. As in the Wikipedia article (and the formulas depend on the matrix sizes!), we can subtract what disturbs, but how should we get rid of products to achieve a sum?