- #1
Frank Castle
- 580
- 23
Apologies for a possibly very basic question. I was recently asked by someone to explain to them the answer to the following classical mechanics (uniform circular motion) problem:
Consider two discs of different radii, attached to one another such that they are concentric, and each containing a rim around its outer edge (such that a ball can fit within the width of the rim). The discs are attached to a spin wheel such that one can freely spin them around, however, since they are attached to one another, they do not move independently.
Suppose now that one has two balls (of identical size and mass) and one places one in the rim of the outer disc (with largest radius) and the other one in the rim of the inner disc (with smallest radius), then one starts the discs spinning. We suppose that the rotation of the discs is fast enough such that the rim of each disc provides a strong enough centripetal force to keep each of the balls following a circular path (each remaining pushed against the rim of of their respective disc).
Since the discs are fixed to one another, such that neither of their motion is independent of one another, they spin with the same angular velocity.
The question is then, as the rotation of the discs starts to slow down, which ball will fall towards the bottom of the disc (and onto the floor) first and why?
(** If it helps, I've attached an image at the bottom of this post to detail the problem pictorially (apologies for the drawing skills! **)My answer to this was that the ball in the rim of the inner disc (with smaller radius) will fall towards the floor first, my reasoning being that the smaller the radius, the greater the tangential velocity of the ball will need to be to maintain a circular path and overcome gravity (analogising to the case of satellite orbit around a planet). Hence, since both discs have the same angular velocity, and the inner disc has a smaller radius, the tangential velocity of the ball in the rim of the inner disc will be smaller and so as the angular velocity decreases (equivalently, the rotation of the disc slows down), the ball in the rim of the inner disc will fall towards the ground first.
I'm fairly sure that this is the correct answer, but the person I was questioned by wasn't satisfied, and furthermore, wanted to see the maths behind the argument.
I have to admit, I'm unsure whether I've done this part correctly. I assumed that it would be easier to work in the rotating reference frame of the disc for the analysis. This being the case, with respect to this reference frame, the ball is at rest and the only force acting on it is gravity, and the (fictitious) centrifugal force, hence we have, $$\mathbf{F}_{gravity} - m_{ball}\mathbf{a}_{centripetal}=\mathbf{F}_{gravity}+\mathbf{F}_{centrifugal}=\mathbf{0}$$ (where ##\mathbf{a}_{centripetal}=\frac{v_{ball}^{2}}{r_{disc}}\hat{\mathbf{r}}##). Thus we require that the magnitude of these two forces be equal $$\frac{GM_{Earth}m_{ball}}{R^{2}}=\frac{m_{ball}v_{ball}^{2}}{R}\Rightarrow v_{ball}^{2}=\frac{GM_{Earth}}{R}$$ This agrees with my answer above. However, the bit I'm sure isn't quite correct, is that actually the radius in the centrifugal force equation should be the radius of the disc, whereas the radius in the gravitational force equation should be that of the Earth.
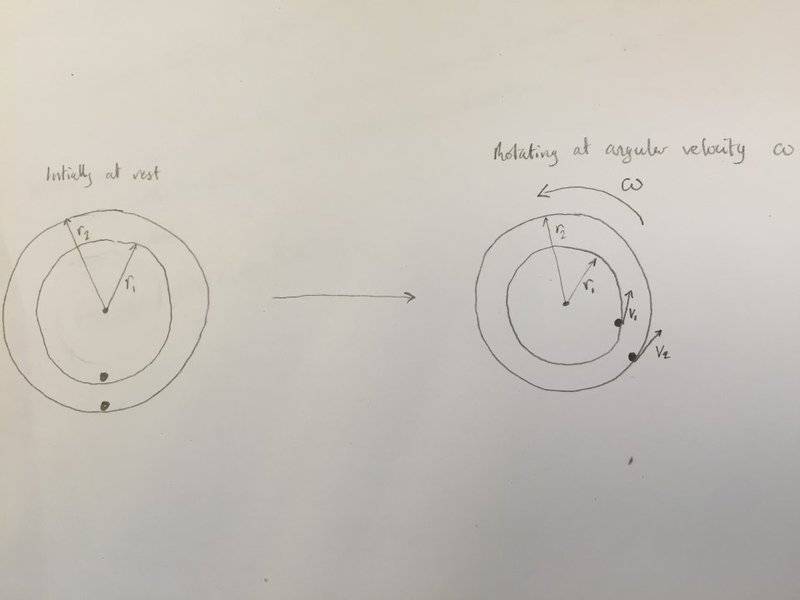
Consider two discs of different radii, attached to one another such that they are concentric, and each containing a rim around its outer edge (such that a ball can fit within the width of the rim). The discs are attached to a spin wheel such that one can freely spin them around, however, since they are attached to one another, they do not move independently.
Suppose now that one has two balls (of identical size and mass) and one places one in the rim of the outer disc (with largest radius) and the other one in the rim of the inner disc (with smallest radius), then one starts the discs spinning. We suppose that the rotation of the discs is fast enough such that the rim of each disc provides a strong enough centripetal force to keep each of the balls following a circular path (each remaining pushed against the rim of of their respective disc).
Since the discs are fixed to one another, such that neither of their motion is independent of one another, they spin with the same angular velocity.
The question is then, as the rotation of the discs starts to slow down, which ball will fall towards the bottom of the disc (and onto the floor) first and why?
(** If it helps, I've attached an image at the bottom of this post to detail the problem pictorially (apologies for the drawing skills! **)My answer to this was that the ball in the rim of the inner disc (with smaller radius) will fall towards the floor first, my reasoning being that the smaller the radius, the greater the tangential velocity of the ball will need to be to maintain a circular path and overcome gravity (analogising to the case of satellite orbit around a planet). Hence, since both discs have the same angular velocity, and the inner disc has a smaller radius, the tangential velocity of the ball in the rim of the inner disc will be smaller and so as the angular velocity decreases (equivalently, the rotation of the disc slows down), the ball in the rim of the inner disc will fall towards the ground first.
I'm fairly sure that this is the correct answer, but the person I was questioned by wasn't satisfied, and furthermore, wanted to see the maths behind the argument.
I have to admit, I'm unsure whether I've done this part correctly. I assumed that it would be easier to work in the rotating reference frame of the disc for the analysis. This being the case, with respect to this reference frame, the ball is at rest and the only force acting on it is gravity, and the (fictitious) centrifugal force, hence we have, $$\mathbf{F}_{gravity} - m_{ball}\mathbf{a}_{centripetal}=\mathbf{F}_{gravity}+\mathbf{F}_{centrifugal}=\mathbf{0}$$ (where ##\mathbf{a}_{centripetal}=\frac{v_{ball}^{2}}{r_{disc}}\hat{\mathbf{r}}##). Thus we require that the magnitude of these two forces be equal $$\frac{GM_{Earth}m_{ball}}{R^{2}}=\frac{m_{ball}v_{ball}^{2}}{R}\Rightarrow v_{ball}^{2}=\frac{GM_{Earth}}{R}$$ This agrees with my answer above. However, the bit I'm sure isn't quite correct, is that actually the radius in the centrifugal force equation should be the radius of the disc, whereas the radius in the gravitational force equation should be that of the Earth.
Last edited:
