Change of variables in double integral

[Happiness]

I get two different answers, $a^2$ and $0.5a^2$, by using two different methods. Which is the correct answer?

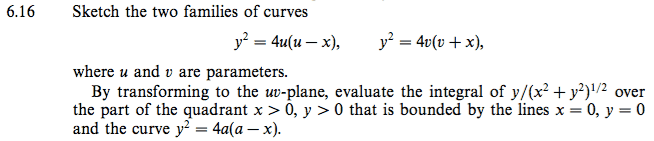
The family of curve for $y^2=4u(u-x)$ is given by the blue curves, and that for $y^2=4v(v+x)$ is given by the red curves.

Method 1:

Evaluate the integral $I$ directly in the xy-plane.

$\int_0^adx\int_0^{\sqrt{4a(a-x)}}dy\,y(x^2+y^2)^{-1/2}$
$=\int_0^adx[(x^2+y^2)^{1/2}]_0^{\sqrt{4a(a-x)}}$
$=\int_0^adx\big((x^2+4a^2-4ax)^{1/2}-|x|\big)$
$=\int_0^adx\big(|x-2a|-|x|\big)$
$=\int_0^adx\big((2a-x)-x\big)$
$=[2ax-x^2]_0^a$
$=a^2$

Method 2:

Evaluate the integral $I$ in the uv-plane. (The blue curves are $u=1$, $u=2$, etc. The red curves are $v=1$, $v=2$, etc.)

First, we express $x$ and $y$ in terms of $u$ and $v$:
$x=u-v$
$y=2\sqrt{uv}$

The above can be easily verified by substituting into $y^2=4u(u-x)$ and $y^2=4v(v+x)$.

$y=-2\sqrt{uv}$ is rejected as the integral is to be done over the region $y>0$.

$I=\frac{1}{4}\int_0^adv\int_0^aduJ\frac{2\sqrt{uv}}{u+v}$, where $J$ is the Jacobian.

The factor $\frac{1}{4}$ is present because the integral is to be done only over the top left quadrant, but $\int_0^adv\int_0^aduJ$ covers the area of the pointed ellipse that extends over all quadrants.

Pointed ellipse (Its left side is the red curve $v=a$ and its right side is the blue curve $u=a$):

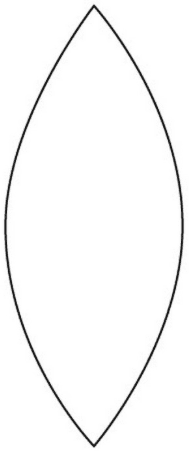
The pointed ellipse is symmetrical about the x and y axes. Thus the area of the pointed ellipse in each quadrant is the same.

$J=\frac{u+v}{\sqrt{uv}}$

$I=\frac{1}{4}\int_0^adv\int_0^adu2=0.5a^2$

Which is the correct answer?

EDIT: In order for $I=a^2$, $\int_0^adv\int_0^aduJ$ must be covering only $\frac{1}{2}$ the area of the pointed ellipse. But why? Has it got to do with the rejection of $y=-2\sqrt{uv}$?

 

[Charles Link]

In your second method, I think your limits on the integrals of u and v is incorrect. The condition $y^2=4a(a-x)$ for a boundary of the region would mean $u=a$. (look at the transformation equations.) Meanwhile putting $x=0$ in both transformation equations gives $u=v$ (or simply by using your solution for $x =u-v$) ,and putting $y=0$ (note: I edited this part) gives $u=0$ and/or $v=0$. I do think this triangular region bounded by these lines should be your region of integration, but do verify this because I computed it somewhat quickly. Since $x=u-v$ and $x>0$, the corresponding region in the u-v plane (of the region from the x-y plane) lies to the right of $u=v$. The rest of your calculations appear to be correct.

 

[Happiness]

putting $y=0$ gives $u=0$ and/or $v=0$.

That's true but I don't see why my integration $\int_0^adv\int_0^aduJ$ covers only half the area of the pointed ellipse.

As $u\to0$, the blue parabola gets narrower and sharper until it becomes a half line that is the negative x axis. Similarly, as $v\to0$, the red parabola gets narrower and sharper until it becomes a half line that is the positive x axis. The takeaway is both $u=0$ and $v=0$ don't give the whole x-axis but only half of it.

Then the overlap of the region $0\leq u\leq a$ and the region $0\leq v\leq a$ is the pointed ellipse. But somehow it should be half of it.

 

[Happiness]

I think one of the assumptions for the change of variable is that the map from xy-plane to uv-plane must be one to one. In order for the map to be one to one, the curve $u=a$ cannot be the whole parabola, but only the part of it that is above the x axis. This is similarly true for the curve $v=a$. Then the integral $\int_0^adv\int_0^aduJ$ covers only half of the pointed ellipse that is above the x axis.

 

[Charles Link]

I think one of the assumptions for the change of variable is that the map from xy-plane to uv-plane must be one to one. In order for the map to be one to one, the curve $u=a$ cannot be the whole parabola, but only the part of it that is above the x axis. This is similarly true for the curve $v=a$. Then the integral $\int_0^adv\int_0^aduJ$ covers only half of the pointed ellipse that is above the x axis.

The $x=0$ boundary in the x-y plane does not give $u=0$. It gives $u=v$. The curve $v=a$ does not represent a boundary prescribed by the original problem. The $u=v$ boundary will make it so that $u=0$ is not a boundary of the region of integration. Your integrations with u going from 0 to "a" and v= 0 to "a" covers twice the region of interest. $x=0$ is a boundary and with $x=u-v$ we must have $u>v$.

 

[Happiness]

The $x=0$ boundary in the x-y plane does not give $u=0$. It gives $u=v$. The curve $v=a$ does not represent a boundary prescribed by the original problem. The $u=v$ boundary will make it so that $u=0$ is not a boundary of the region of integration. Your integrations with u going from 0 to "a" and v= 0 to "a" covers twice the region of interest. $x=0$ is a boundary and with $x=u-v$ we must have $u>v$.

What would the limits of your integration be for $\int du$ and $\int dv$?

 

[Charles Link]

Since the integrand is constant in the integration, you can just compute the area of the triangle, but let's put in the limits. Do v first from 0 to "u" and let u go from 0 to a. If you integrate u first, it goes from v to a and then v goes from 0 to a.

 

[Happiness]

Since the integrand is constant in the integration, you can just compute the area of the triangle, but let's put in the limits. Do v first from 0 to "u" and let u go from 0 to a. If you integrate u first, it goes from v to a and then v goes from 0 to a.

These limits satisfy $u>v$, which corresponds to $x>0$. This region would be the right side of the pointed ellipse, covering the first and fourth quadrants. So if we want the integration to be done only over the first quadrant, we have to multiply a factor of $\frac{1}{2}$, giving us $0.5a^2$, the same answer as method 2 of post #1.

In other words, the original question of post #1 is now phrased in another form: Why is $\int_0^adu\int_0^udvJ$ covering the first quadrant of the pointed ellipse instead of both the first and fourth quadrants?

 

[Charles Link]

It's $I=\int\limits_{0}^{a}du \int\limits_{0}^{v}dv J f(u,v)$, but in any case it covers the complete first quadrant in the x-y plane. x=0 in the x-y plane does not correspond to u=0. It corresponds to u=v. The y=0 boundary has v=0.

 

[Happiness]

It's $I=\int\limits_{0}^{a}du \int\limits_{0}^{v}dv J f(u,v)$, but in any case it covers the complete first quadrant in the x-y plane. x=0 in the x-y plane does not correspond to u=0. It corresponds to u=v.

You get $u>v$ from $x>0$, right? $x>0$ means positive x values, which cover both top right quadrant and bottom right quadrant. So why doesn't $\int\limits_{0}^{a}du \int\limits_{0}^{u}dv J$ cover the bottom right quadrant?

 

[Charles Link]

You get $u>v$ from $x>0$, right? $x>0$ means positive x values, which cover both top right quadrant and bottom right quadrant. So why doesn't $\int\limits_{0}^{a}du \int\limits_{0}^{u}dv J$ cover the bottom right quadrant?

On a given parabola u=constant, to get the y<0 values, v must be less than 0. If v>0, (which we have in our u-v integration), for x>0, I think y>0, so it is in the first quadrant...editing... let me look this over me carefully...

 

[Happiness]

On a given parabola u=constant, to get the y<0 values, v must be less than 0. If v>0, (which we have in our u-v integration), for x>0, I think y>0, so it is in the first quadrant.

$y$ was supposed to be $y=\pm2\sqrt{uv}$. So the integrand $\frac{y}{(x^2+y^2)^{1/2}}=\frac{\pm2\sqrt{uv}}{u+v}$. If we make the integrand $\frac{2\sqrt{uv}}{u+v}$, that means we are calculating $\int du\int dvJ|\frac{y}{(x^2+y^2)^{1/2}}|$.

 

[Charles Link]

$y$ was supposed to be $y=\pm2\sqrt{uv}$. So the integrand $\frac{y}{(x^2+y^2)^{1/2}}=\frac{\pm2\sqrt{uv}}{u+v}$. If we make the integrand $\frac{2\sqrt{uv}}{u+v}$, that means we are calculating $\int du\int dvJ|\frac{y}{(x^2+y^2)^{1/2}}|$.

I think I have an explanation. Select the curves (in the x-y plane) $u=a$ and $u= a/2$ and $v=a$ and $v= a/2$. Now find the region $u>v$ that covers $a/2<u<a$ and $a/2<v<a$. You will see that there are actually two disconnected regions=one in the first quadrant and one in the 4th quadrant. Apparently a single u-v integration only gives you one of these regions. You select the one in the first quadrant. It may take additional analysis to figure out the "hows" and "whys" but perhaps this latest input will help. (When you choose u=0 and v=0, (instead of u=a/2 and v=a/2), the two regions are still disconnected.) And, yes, you are correct=in the u-v integration, there seems to be nothing that selects the first quadrant rather than the fourth quadrant of the x-y plane. It appears though that these regions are separate and disconnected.

 

[Charles Link]

I think post #13 successfully answers the question of how the u-v integral over the limits mentioned above gives a result that essentially is in the first quadrant of the x-y plane rather than covering both first and fourth quadrant. I welcome your feedback. Is the explanation reasonably sufficient? It does give the correct answer that was computed in your post #1 method 1. The transformation in this problem appears to give two separate regions in the x-y plane for a given region in the u-v plane, so there is some ambiguity present that requires careful analysis of any results that are generated. I believe a given u-v integration will equate (with the Jacobian) to an integration over a single x-y region.

 

[Happiness]

Post #13 is saying that the map between the uv-plane and the xy-plane should map a simply connected region to a simply connected region. If this claim is true, it will make it seems plausible (but it does not dictate) that the uv integration $\int_0^a du\int_0^u dvJ$ covers either the first quadrant or the fourth quadrant but not both. It does not dictate that because we are still mapping a simply connected region in the uv-plane to a simply connected region in the xy-plane (which is both first and fourth quadrants joined together).

I think the explanation got to do with the map between the uv-plane and the xy-plane having the requirement of being a one-to-one correspondence (bijective). Currently, if we take $y=\pm2\sqrt{uv}$, one point on the uv-plane is being mapped to two points on the xy-plane (for $u\neq0$ and $v\neq0$). Consequently, two points will be mapped to four points. And we may argue that one region will be mapped to two regions, or one region of area $A$ will be mapped to one region (or regions) of total area $2A$. In other words, when the map is not bijective, the change of variables $\int dx\int dy\to\int du\int dvJ$ does not conserve area. If area is not conserved, naturally, we expect methods 1 and 2 to produce different answers.

 

[Charles Link]

Post #13 is saying that the map between the uv-plane and the xy-plane should map a simply connected region to a simply connected region. If this claim is true, it will make it seems plausible (but it does not dictate) that the uv integration $\int_0^a du\int_0^u dvJ$ covers either the first quadrant or the fourth quadrant but not both. It does not dictate that because we are still mapping a simply connected region in the uv-plane to a simply connected region in the xy-plane (which is both first and fourth quadrants joined together).

I think the explanation got to do with the map between the uv-plane and the xy-plane having the requirement of being a one-to-one correspondence (bijective). Currently, if we take $y=\pm2\sqrt{uv}$, one point on the uv-plane is being mapped to two points on the xy-plane (for $u\neq0$ and $v\neq0$). Consequently, two points will be mapped to four points. And we may argue that one region will be mapped to two regions, or one region of area $A$ will be mapped to one region (or regions) of total area $2A$. In other words, when the map is not bijective, the change of variables $\int dx\int dy\to\int du\int dvJ$ does not conserve area.

I agree with you here. One question is, can we rely on the answer we get in a u-v integration as an alternative to the x-y integration? I think the answer is yes, but it needs to be inspected carefully.

 

[Happiness]

I agree with you here. One question is, can we rely on the answer we get in a u-v integration as an alternative to the x-y integration? I think the answer is yes, but it needs to be inspected carefully.

I suppose what you are asking is whether methods 1 and 2 give the same answer. They would if area is conserved. And that would require the map to be bijective. But the current map's component function $y=\pm2\sqrt{uv}$ isn't bijective. So we have to modify it to one that is bijective in order to have methods 1 and 2 give the same answer.

 

[Charles Link]

They do give the same answer if you take the function integrated over a single x-y region (e.g. in the first quadrant) and compare it to the u-v region with the function multiplied by the Jacobian. In method 2 with the u-v limits as I selected them, I did get $I=a^2$. I didn't need to introduce any other factors.

 

[Happiness]

This may provide an explanation.

There is another problem with the map $y^2=4uv$, apart from it being not 1-1. It is that $y$ is not differentiable with respect to $u$ and to $v$ when $y=0$.

Recall that in order to use the substitution

$y$ has to be differentiable.

 

[Charles Link]

It gave us a correct answer. It appears this is one of those where the answer was not guaranteed.