Comparing Methods for Initial Value Problem

[evinda]

Hello! (Wave)

We consider the initial value problem:

$$x'(t)=-5x(t)-2y(t), t \in [0,1] \\ y'(t)=-2x(t)-100y(t), t \in [0,1] \\ x(0)=1, y(0)=1.$$

I want to solve the above problem using the forward Euler method, the trapezoid method and the backward Euler method and to represent in common graphs the corresponding values of $(x^n)^2+(y^n)^2$.

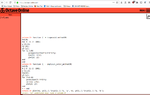
First of all, the formula for the approximation $y$ that we have using the backward Euler method is the following, right?

[m]y=inv(eye(2)-h*A)*y [/m]

where [m]A=[-5 -2;-2 -100][/m], right?

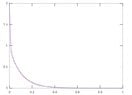
Then, I get the following graph for the approximations $(x^n)^2+(y^n)^2$.

View attachment 8113

The graphs are approximately the same, aren't they?

How can we deduce from this graph which method is better? (Thinking)

 

[I like Serena]

First of all, the formula for the approximation $y$ that we have using the backward Euler method is the following, right?

[m]y=inv(eye(2)-h*A)*y [/m]

where [m]A=[-5 -2;-2 -100][/m], right?

Indeed. (Nod)

Then, I get the following graph for the approximations $(x^n)^2+(y^n)^2$.

The graphs are approximately the same, aren't they?

How can we deduce from this graph which method is better? (Thinking)

I'm not sure if we can say all that much from the graph.

The best I can come up with, is that we can expect the graph to be smooth, so the red graph can't be right.

And we can expect the trapezoidal graph to be most accurate, since it's a 2nd order approximation.
So we can compare forward Euler and backward Euler with each other by looking how close they are to the trapezoidal graph.
Or if we add the graph of the exact solution, we can compare all methods with that graph.

It would be best if we subtract the exact solution from approximations before plotting them, then we see directly which one is best, since then we'd actually be looking at the errors. (Thinking)

Or instead of the exact solution, we can use Octave's ODE solver (which will use some variant of Runge-Kutta) to find:

A=[-5 -2;-2 -100];
y0=[1;1];
N=100;
h=1/N;
tt=(0:N)*h;
yyLsode = lsode(@(y,t) A*y, y0, tt)';

(Nerd)

 

[evinda]

The best I can come up with, is that we can expect the graph to be smooth, so the red graph can't be right.

I have written the following code for the trapezoid method:

y=[1;1];
t2=[0];
y2=[y];
for (i=1:N)
      y=(eye(2)+h*A+h^2/2*A^2)*y;
      t2=[t2, i*h];
      y2=[y2, y];
end

So is something wrong? (Thinking)

 

[I like Serena]

I have written the following code for the trapezoid method:

y=[1;1];
t2=[0];
y2=[y];
for (i=1:N)
      y=(eye(2)+h*A+h^2/2*A^2)*y;
      t2=[t2, i*h];
      y2=[y2, y];
end

So is something wrong? (Thinking)

Looks fine to me.
What do you think is wrong with it? (Wondering)

 

[evinda]

Looks fine to me.
What do you think is wrong with it? (Wondering)

I thought it was wrong, because you said that the red graph can't be right and I thought it corresponds to the trapezoid method. But now I saw that it corresponds to the forward Euler method. But I think I applied it correctly. Is the red graph maybe like that because this method isn't exact enough? (Thinking)

 

[I like Serena]

I thought it was wrong, because you said that the red graph can't be right and I thought it corresponds to the trapezoid method. But now I saw that it corresponds to the forward Euler method. But I think I applied it correctly. Is the red graph maybe like that because this method isn't exact enough? (Thinking)

Indeed.
It wouldn't be exact enough, showing a graph that is not smooth (it has a bend in it) even though the other approximations do seem to be smooth enough. (Thinking)

 

[evinda]

Indeed.
It wouldn't be exact enough, showing a graph that is not smooth (it has a bend in it) even though the other approximations do seem to be smooth enough. (Thinking)

Ok. But why isn't there a difference between the graph of the trapezoid method and the graph of the backward Euler method, although the first one is a 2nd order method and the latter a 1st order method? (Thinking)

 

[I like Serena]

Ok. But why isn't there a difference between the graph of the trapezoid method and the graph of the backward Euler method, although the first one is a 2nd order method and the latter a 1st order method? (Thinking)

Wouldn't that be because backward Euler is also less exact than the trapezoid method? (Wondering)

 

[evinda]

Wouldn't that be because backward Euler is also less exact than the trapezoid method? (Wondering)

But how is this seen at the graph? (Thinking)

 

[I like Serena]

But how is this seen at the graph? (Thinking)

I don't think we can.
Not unless we compare it with either the real solution, or a better approximation. (Thinking)

 

[evinda]

I don't think we can.
Not unless we compare it with either the real solution, or a better approximation. (Thinking)

Which command could we use in [m]matlab[/m] to find the real solution of the initial value problem? (Thinking)

 

[I like Serena]

Which command could we use in [m]matlab[/m] to find the real solution of the initial value problem? (Thinking)

We can write $A$ as $A=VDV^{-1}$, where $D$ is a diagonal matrix with eigenvalues $\lambda_i$ and $V$ is the matrix of corresponding eigenvectors.
Consequently, the solution of $y'=Ay,\ y(0)=y_0$ is:
$$y(t)=V\left[\sum_i(V^{-1}y_0)_i\cdot (e^{\lambda_i t})\mathbf e_i\right]$$
(I'm leaving out a couple of intermediate steps. (Blush))

In MatLab/Octave terms:

A=[-5 -2;-2 -100];
y0=[1;1];
[V D] = eig(A);
exactSolution = @(t) V*(V\y0.*exp(diag(D)*t));

N=100;
h=1/N;
tt=(0:N)*h;
yyExact = exactSolution(tt);

(Thinking)

 

[evinda]

Indeed.
It wouldn't be exact enough, showing a graph that is not smooth (it has a bend in it) even though the other approximations do seem to be smooth enough. (Thinking)

I am a little confused now. Why does the fact that the graph is not smooth show that the method is not exact? Couldn't it be that the graph of $x^2+y^2$ is indeed not smooth? (Thinking)

 

[I like Serena]

I am a little confused now. Why does the fact that the graph is not smooth show that the method is not exact? Couldn't it be that the graph of $x^2+y^2$ is indeed not smooth? (Thinking)

Suppose the graph is not smooth because, say, $y''(t)$ has a discontinuity at $t_0$ with $t_0\in [0,1]$.
This is what the red graph has.
Then $y'(t)$ is not differentiable at $t_0$.
But we know that $y'(t_0)=Ay(t_0)$ and that $y$ is defined on $[0,1]$.
This is a contradiction.
Therefore $y''$ is continuous on $[0,1]$ and the graph cannot have a bend in it. (Thinking)

 

[evinda]

Suppose the graph is not smooth because, say, $y''(t)$ has a discontinuity at $t_0$ with $t_0\in [0,1]$.
This is what the red graph has.
Then $y'(t)$ is not differentiable at $t_0$.
But we know that $y'(t_0)=Ay(t_0)$ and that $y$ is defined on $[0,1]$.
This is a contradiction.
Therefore $y''$ is continuous on $[0,1]$ and the graph cannot have a bend in it. (Thinking)

How is $y''(t)$ related to the graph? I am confused right now. (Worried)

 

[I like Serena]

How is $y''(t)$ related to the graph? I am confused right now. (Worried)

A jump discontinuity in $y''$ shows up as a bend in the graph of $y$, doesn't it?

EDIT: my mistake, a jump discontinuity in $y'$ shows up as a bend in the graph of $y$, doesn't it? (Wondering)

 

[evinda]

A jump discontinuity in $y''$ shows up as a bend in the graph of $y$, doesn't it?

EDIT: my mistake, a jump discontinuity in $y'$ shows up as a bend in the graph of $y$, doesn't it? (Wondering)

The bend appears at the graph that represents the approximations $(x^n)^2+(y^n)^2$ that we get, when applying the forward Euler method. Since a bend appears, this means that either $(x^n)'$ or $(y^n)'$ is discontinuous at some point $t_0$, right? It holds that $Y'(t)=AY(t)$, where $Y(t)=(x(t),y(t))$. But from this we don't get that $x'(t)$ and $y'(t)$ are continuous, do we? (Thinking)

 

[I like Serena]

The bend appears at the graph that represents the approximations $(x^n)^2+(y^n)^2$ that we get, when applying the forward Euler method. Since a bend appears, this means that either $(x^n)'$ or $(y^n)'$ is discontinuous at some point $t_0$, right? It holds that $Y'(t)=AY(t)$, where $Y(t)=(x(t),y(t))$. But from this we don't get that $x'(t)$ and $y'(t)$ are continuous, do we? (Thinking)

We do.
For the problem to be well-defined, $Y$ must be differentiable on $[0,1]$, implying that $Y$ is continuous as well.
$Y'=AY$ is a linear combination of continuous functions, which means that $Y'$ is continuous as well. (Thinking)

 

[evinda]

We do.
For the problem to be well-defined, $Y$ must be differentiable on $[0,1]$, implying that $Y$ is continuous as well.
$Y'=AY$ is a linear combination of continuous functions, which means that $Y'$ is continuous as well. (Thinking)

Ah I see... (Nod) Thanks a lot! (Smile)

 

[evinda]

Hey! (Blush)

We have the system $\Psi '(t)=A\Psi(t)=:\Phi (t,\psi )$, where $\psi$ is the vector $(x(t), y(t))$.

Then to show that the right side of that system satisfies the one sided Lipschitz condition, we have to show that
\begin{equation*}\left (\Phi (t,\phi )-\Phi (t,
\tilde{\psi}), \psi-\tilde{\psi}\right )\leq L(t)\|\psi -\tilde{\psi}\|^2.\end{equation*}

We have \begin{equation*}\left (\Phi (t,\phi )-\Phi (t,
\tilde{\psi}), \psi-\tilde{\psi}\right )=\left (A\left (\psi-\tilde{\psi}\right ), \psi-\tilde{\psi}\right )\end{equation*}

Let $\psi-\tilde{\psi}=(w_1,w_2)\in \mathbb{R}^2$.

The above inner product is less that $-3w_1^2-98w_2^2$, or not?

Then we have that \begin{equation*}\left (\Phi (t,\phi )-\Phi (t,
\tilde{\psi}), \psi-\tilde{\psi}\right )\leq -3w_1^2-98w_2^2\leq -3w_1^2-3w_2^2=-3\left (w_1^2+w_2^2\right )=-3\|\psi-\tilde{\psi}\|\end{equation*}
and so the one sided Lipschitz condition is satisfied with constant $-3$.Am I right? (Thinking)

 

[I like Serena]

Hey! (Blush)

We have the system $\Psi '(t)=A\Psi(t)=:\Phi (t,\psi )$, where $\psi$ is the vector $(x(t), y(t))$.

Then to show that the right side of that system satisfies the one sided Lipschitz condition, we have to show that
\begin{equation*}\left (\Phi (t,\phi )-\Phi (t,
\tilde{\psi}), \psi-\tilde{\psi}\right )\leq L(t)\|\psi -\tilde{\psi}\|^2.\end{equation*}

We have \begin{equation*}\left (\Phi (t,\phi )-\Phi (t,
\tilde{\psi}), \psi-\tilde{\psi}\right )=\left (A\left (\psi-\tilde{\psi}\right ), \psi-\tilde{\psi}\right )\end{equation*}

Let $\psi-\tilde{\psi}=(w_1,w_2)\in \mathbb{R}^2$.

The above inner product is less that $-3w_1^2-98w_2^2$, or not?

Hey evinda!

Don't we have:
\begin{equation*}\left (\Phi (t,\psi )-\Phi (t,
\tilde{\psi}), \psi-\tilde{\psi}\right )=\left (A\Psi-A\tilde{\Psi}, \psi-\tilde{\psi}\right )
=A\left (\Psi-\tilde{\Psi}, \psi-\tilde{\psi}\right )
\end{equation*}
I'm assuming $\Psi$ is different from $\phi$. Isn't it? (Wondering)

Either way, we can't just conclude that this is less than $-3w_1^2-98w_2^2$ can we? (Worried)
Where does that expression come from?
Is there more information for the problem?

Then we have that \begin{equation*}\left (\Phi (t,\phi )-\Phi (t,
\tilde{\psi}), \psi-\tilde{\psi}\right )\leq -3w_1^2-98w_2^2\leq -3w_1^2-3w_2^2=-3\left (w_1^2+w_2^2\right )=-3\|\psi-\tilde{\psi}\|\end{equation*}
and so the one sided Lipschitz condition is satisfied with constant $-3$.

If we assume the inequality, then I think that is correct yes. (Dull)

 

[evinda]

Hey evinda!

Don't we have:
\begin{equation*}\left (\Phi (t,\psi )-\Phi (t,
\tilde{\psi}), \psi-\tilde{\psi}\right )=\left (A\Psi-A\tilde{\Psi}, \psi-\tilde{\psi}\right )
=A\left (\Psi-\tilde{\Psi}, \psi-\tilde{\psi}\right )
\end{equation*}
I'm assuming $\Psi$ is different from $\phi$. Isn't it? (Wondering)

Either way, we can't just conclude that this is less than $-3w_1^2-98w_2^2$ can we? (Worried)
Where does that expression come from?
Is there more information for the problem?
If we assume the inequality, then I think that is correct yes. (Dull)

Let $\Psi '(t)=A\Psi(t)=:\Phi (t,\psi )$.

Then don't we have that \begin{equation*}\left (\Phi (t,\psi )-\Phi (t,
\tilde{\psi}), \psi-\tilde{\psi}\right )=\left (A\psi-
A\tilde{\psi}, \psi-\tilde{\psi}\right )=\left (A\left (\psi-\tilde{\psi}\right ), \psi-\tilde{\psi}\right )\end{equation*} ? We have that for $\Psi \in \mathbb{R}^2$ it holds the following \begin{align*}(A\Psi, \Psi )&=-5\psi_1^2-4\psi_1\psi_2-100\psi_2^2\\ & \leq -5\psi_1^2+2\cdot 2|\psi_1\psi_2|-100\psi_2^2 \\ & \leq -5\psi_1^2+2\psi_1^2+2\psi_2^2-100\psi_2^2\\ & =-3\psi_1^2-98\psi_2^2\end{align*} or not?

Let $\psi-\tilde{\psi}=(w_1,w_2)\in \mathbb{R}^2$.

Then we have that $\left (\Phi (t,\phi )-\Phi (t,
\tilde{\psi}), \psi-\tilde{\psi}\right )$ is less that $-3w_1^2-98w_2^2$, right? (Thinking)

 

[I like Serena]

Let $\Psi '(t)=A\Psi(t)=:\Phi (t,\psi )$.

Then don't we have that \begin{equation*}\left (\Phi (t,\psi )-\Phi (t,
\tilde{\psi}), \psi-\tilde{\psi}\right )=\left (A\psi-
A\tilde{\psi}, \psi-\tilde{\psi}\right )=\left (A\left (\psi-\tilde{\psi}\right ), \psi-\tilde{\psi}\right )\end{equation*} ?

Isn't $\Psi$ different from $\psi$?
That is, isn't $\Phi (t,\psi ) =A\Psi(t) \ne A\psi(t)$? (Worried)

We have that for $\Psi \in \mathbb{R}^2$ it holds the following \begin{align*}(A\Psi, \Psi )&=-5\psi_1^2-4\psi_1\psi_2-100\psi_2^2\\ & \leq -5\psi_1^2+2\cdot 2|\psi_1\psi_2|-100\psi_2^2 \\ & \leq -5\psi_1^2+2\psi_1^2+2\psi_2^2-100\psi_2^2\\ & =-3\psi_1^2-98\psi_2^2\end{align*} or not?

How did you get the equality $(A\Psi, \Psi )=-5\psi_1^2-4\psi_1\psi_2-100\psi_2^2$ ? (Wondering)

 

[evinda]

Let's start from the beginning with more details. (Blush)

We have the system in matrix form: $$\Psi '(t)=A\Psi(t)=\begin{pmatrix}-5 & -2 \\ -2 & -100\end{pmatrix}\Psi (t)$$ where $\Psi (t)=\begin{pmatrix}x(t)\\ y(t)\end{pmatrix}$.

To check the Lipschitz condition we define the function $\Phi (t,\Psi ):=A\Psi(t)$, or not?

Then do we have that \begin{equation*}\left (\Phi (t,\Psi )-\Phi (t,
\tilde{\Psi}), \Psi-\tilde{\Psi}\right )=\left (A\Psi-
A\tilde{\Psi}, \Psi-\tilde{\Psi}\right )=\left (A\left (\Psi-\tilde{\Psi}\right ), \Psi-\tilde{\Psi}\right )\end{equation*} right For an arbitrary $W =(w_1,w_2)^T\in \mathbb{R}^2$ we have the following inner product \begin{align*}(AW, W )&=\left ( \begin{pmatrix}-5 & -2 \\ -2 & -100\end{pmatrix}\begin{pmatrix}w_1\\ w_2\end{pmatrix}, \begin{pmatrix}w_1\\ w_2\end{pmatrix}\right )\\ &=\left ( \begin{pmatrix}-5w_1-2w_2 \\ -2w_1-100w_2 \end{pmatrix}, \begin{pmatrix}w_1\\ w_2\end{pmatrix}\right ) \\ &= \begin{pmatrix}-5w_1-2w_2 \\ -2w_1-100w_2 \end{pmatrix}\cdot \begin{pmatrix}w_1\\ w_2\end{pmatrix} \\ &= (-5w_1-2w_2)w_1+(-2w_1-100w_2)w_2 \\ & = -5w_1^2-4w_1w_2-100w_2^2\\ & \leq -5w_1^2+2\cdot 2|w_1w_2|-100w_2^2 \\ & \leq -5w_1^2+2w_1^2+2w_2^2-100w_2^2\\ & =-3w_1^2-98w_2^2\end{align*}

This holds also for $W=\Psi-\tilde{\Psi}$.

Then we have that $$\left (\Phi (t,\Psi )-\Phi (t,
\tilde{\Psi}), \Psi-\tilde{\Psi}\right )\leq -3w_1^2-98w_2^2$$

Are my thoughts right so far? (Thinking)

 

[I like Serena]

Looks all correct to me. (Nod)

 

[evinda]

I tried to plot the following code but I get the following message:
"error: invalid use of script in index expression"

What does this mean? (Thinking)

The code is the following:

function [] = trapezoid_method(N)
h=1/N;
A=[-5 -2;-2 -100];
y=[1;1];
t2=[0];
y2=[y];
for (i=1:N)
      y=(eye(2)+h*A+h^2/2*A^2)*y;
      t2=[t2, i*h];
      y2=[y2, y];
end

function [] = implicit_euler_method(N)
h=1/N;
A=[-5 -2;-2 -100];
y=[1;1];
t3=[0];
y3=[y];
for (i=1:N)
    y=inv(eye(2)-h*A)*y;
    t3=[t3, i*h];
    y3=[y3, y];
end

plot(t2, y2(1,:).^2+y2(2,:).^2, 'y', t3, y3(1,:).^2+y3(2,:).^2, 'b');

 

[I like Serena]

At first look it seems to me that the problem is that the functions do not return anything.
The variables inside those functions, that are assigned values, are local to the function.
So when you plot those variables, you'd get an error because none of those variables have an actual value. (Worried)

 

[evinda]

At first look it seems to me that the problem is that the functions do not return anything.
The variables inside those functions, that are assigned values, are local to the function.
So when you plot those variables, you'd get an error because none of those variables have an actual value. (Worried)

Ah ok...How can we change this? How do the variables get a value? (Thinking)

 

[I like Serena]

Ah ok...How can we change this? How do the variables get a value? (Thinking)

A function definition and its use look like this:

function [m,s] = stat(x)
    n = length(x);
    m = sum(x)/n;
    s = sqrt(sum((x-m).^2/n));
end function

values = [12.7, 45.4, 98.9, 26.6, 53.1];
[ave,stdev] = stat(values)

(Malthe)

Perhaps it should be something like this?

function [t2, y2] = trapezoid_method(N)
   h=1/N;
   A=[-5 -2;-2 -100];
   y=[1;1];
   t2=[0];
   y2=[y];
   for (i=1:N)
      y=(eye(2)+h*A+h^2/2*A^2)*y;
      t2=[t2, i*h];
      y2=[y2, y];
   end for
end function

[t2, y2] = trapezoid_method(10)

(Wondering)

 

[evinda]

A function definition and its use look like this:

function [m,s] = stat(x)
    n = length(x);
    m = sum(x)/n;
    s = sqrt(sum((x-m).^2/n));
end function

values = [12.7, 45.4, 98.9, 26.6, 53.1];
[ave,stdev] = stat(values)

(Malthe)

Perhaps it should be something like this?

function [t2, y2] = trapezoid_method(N)
   h=1/N;
   A=[-5 -2;-2 -100];
   y=[1;1];
   t2=[0];
   y2=[y];
   for (i=1:N)
      y=(eye(2)+h*A+h^2/2*A^2)*y;
      t2=[t2, i*h];
      y2=[y2, y];
   end for
end function

[t2, y2] = trapezoid_method(10)

(Wondering)

Unfortunately, I still get the same error message... (Shake)

 

[I like Serena]

I tried:

t2=[1 2];
y2=[3 4; 5 6];
plot(t2, y2(1,:).^2+y2(2,:).^2, 'y');

That works... (Thinking)

Did you perhaps put those functions in script files?
Or are you running the code on the prompt?

Btw, your current functions are not syntactically correct since 'for' has an 'end', but 'function' does not have an 'end'. (Worried)

 

[evinda]

I tried:

t2=[1 2];
y2=[3 4; 5 6];
plot(t2, y2(1,:).^2+y2(2,:).^2, 'y');

That works... (Thinking)

Did you perhaps put those functions in script files?
Or are you running the code on the prompt?

Btw, your current functions are not syntactically correct since 'for' has an 'end', but 'function' does not have an 'end'. (Worried)

I wrote that code in a script .m and when I run it it is asked to enter a value for N. I give for example 100 and then I get the error message.

I did that in https://octave-online.net/

So, when you run that code it is executed normally without any error? (Thinking)

 

[I like Serena]

I wrote that code in a script .m and when I run it it is asked to enter a value for N. I give for example 100 and then I get the error message.

I did that in https://octave-online.net/

So, when you run that code it is executed normally without any error?

If I copy and paste your code in octave-online, I don't get any response. (Worried)

I expected that since those functions are not terminated with the [M]end[/M] that should come after. (Nerd)

What did you put in octave-online exactly?
How did you get the error? (Wondering)

 

[evinda]

There are two functions that I want to plot. Here you can see the functions I wrote then I press RUN and enter 100 as the value for N and as you can see I get again an error message. What have I done wrong? (Thinking)

View attachment 9067

 

[I like Serena]

There are two functions that I want to plot. Here you can see the functions I wrote then I press RUN and enter 100 as the value for N and as you can see I get again an error message. What have I done wrong?

If we put a function into a file named [M]ex.m[/M], then that file must contain exactly a function named [M]ex[/M] and no other statements.
Since that is not the case, we get an error that is unfortunately not very descriptive. (Worried)If we copy and paste your code into the regular command prompt of Octave online, we get:
View attachment 9068

Now we get the error that the variables are not known as I explained. (Nerd)Alternatively, we can create a new file named [M]trapezoid_method.m[/M].
Put the code of the function in there, and only that function.
Click the save button.
Type [M]trapezoid_method(10)[/M] on the command prompt.
Now it will execute the function as desired. (Happy)