- #1
Terrell
- 317
- 26
Homework Statement
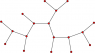
i've attached an image of the given problem. please see below
Homework Equations
tax revenue - maintenance cost = net revenue. net revenue can never be negative
The Attempt at a Solution
i've tried setting (p1)^2 for the revenue of a random city,
(p2)^2 for the revenue of the city that the other connects to,
then (p1)(p2) for the maintenance cost of the road that connects the two.
revenue: (p1)^2 + (p2)^2 + (p3)^2 + ... + (pn)^2
maintenance cost: (p1)(p2) + (p1)(p3) + ... (i guess this depends on how the distribution of maintenance cost will be like)
we can also deduce from the queen's decree that tree graphs cannot connect with loops because it violates the "there can only be one way from one city to any other city" law.
i'm having difficulty generalizing because the problem asks for the maximum number of cities REGARDLESS of population and road design. (road design is really vague for me).