- #1
deuteron
- 51
- 12
- Homework Statement
- The bead can glide freely along the rod rotating with constant angular velocity on the xy-plane. What is the constraint force exerted by the rod?
- Relevant Equations
- ##\dot\varphi=\omega##
Consider the following setup
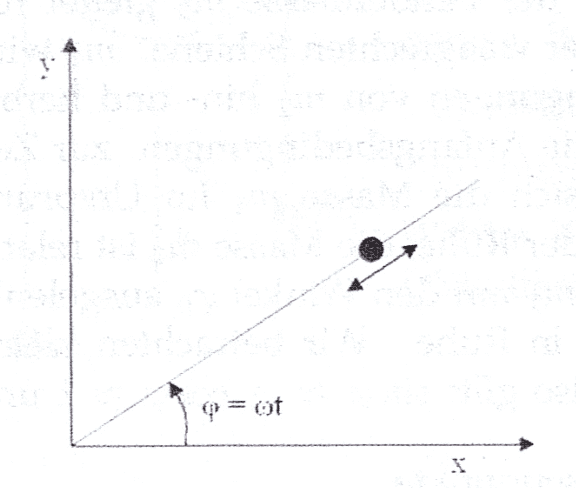
where the bead can glide along the rod without friction, and the rod rotates with a constant angular velocity ##\omega##, and we want to find the constraint force using Lagrange multipliers.
I chose the generalized coordinates ##q=\{r,\varphi\}## and the constraint equation ##f## to be ##\varphi=\omega t##
We get the Lagrangian to be
$$\mathcal L= \frac 12m (\dot s^2 +s^2 \dot\varphi^2)- mgs\sin\varphi.$$
For the equation of motion, I got:
$$\begin{align}
\frac {\partial\mathcal L}{\partial \varphi}&= -mgs\cos\varphi\\
\frac{\partial\mathcal L}{\partial\dot\varphi}&= ms^2\dot \varphi\\
\frac d{dt}\frac {\partial\mathcal L}{\partial\dot\varphi}&= 2ms\dot s\dot \varphi +ms^2\ddot\varphi\\
\Rightarrow\ 2ms\dot s \omega + mgs\cos(\omega t)&=\lambda\frac {\partial f}{\partial\varphi} = \lambda\\
\frac{\partial\mathcal L}{\partial s}&= ms\dot\varphi^2 -mg\sin\varphi\\
\frac d{dt}\frac{\partial\mathcal L}{\partial\dot s}&= m\ddot s\\
\Rightarrow\ m\ddot s &= ms\dot \varphi^2 =ms\dot\omega^2\ \Rightarrow\ s(t)=s_0 \cos(\omega t)
\end{align}$$
and substituting $s(t)=s_0 \cos(\omega t)$ back to the equation for ##\varphi## results in:
$$-2ms_0^2\omega^2\cos(\omega t)\sin(\omega t) +mgs_0\cos^2(\omega t)=\lambda$$
and the constraint force is ##C=\lambda\frac {\partial f}{\partial\varphi}+\lambda \frac{\partial f}{\partial s} = -2ms_0^2\omega^2\cos(\omega t)\sin(\omega t) +mgs_0\cos^2(\omega t)##
However, this is not true and the force is supposed to be ##C= 2m\omega^2 s_0 \sinh(\omega t)##, what am I doing wrong?
where the bead can glide along the rod without friction, and the rod rotates with a constant angular velocity ##\omega##, and we want to find the constraint force using Lagrange multipliers.
I chose the generalized coordinates ##q=\{r,\varphi\}## and the constraint equation ##f## to be ##\varphi=\omega t##
We get the Lagrangian to be
$$\mathcal L= \frac 12m (\dot s^2 +s^2 \dot\varphi^2)- mgs\sin\varphi.$$
For the equation of motion, I got:
$$\begin{align}
\frac {\partial\mathcal L}{\partial \varphi}&= -mgs\cos\varphi\\
\frac{\partial\mathcal L}{\partial\dot\varphi}&= ms^2\dot \varphi\\
\frac d{dt}\frac {\partial\mathcal L}{\partial\dot\varphi}&= 2ms\dot s\dot \varphi +ms^2\ddot\varphi\\
\Rightarrow\ 2ms\dot s \omega + mgs\cos(\omega t)&=\lambda\frac {\partial f}{\partial\varphi} = \lambda\\
\frac{\partial\mathcal L}{\partial s}&= ms\dot\varphi^2 -mg\sin\varphi\\
\frac d{dt}\frac{\partial\mathcal L}{\partial\dot s}&= m\ddot s\\
\Rightarrow\ m\ddot s &= ms\dot \varphi^2 =ms\dot\omega^2\ \Rightarrow\ s(t)=s_0 \cos(\omega t)
\end{align}$$
and substituting $s(t)=s_0 \cos(\omega t)$ back to the equation for ##\varphi## results in:
$$-2ms_0^2\omega^2\cos(\omega t)\sin(\omega t) +mgs_0\cos^2(\omega t)=\lambda$$
and the constraint force is ##C=\lambda\frac {\partial f}{\partial\varphi}+\lambda \frac{\partial f}{\partial s} = -2ms_0^2\omega^2\cos(\omega t)\sin(\omega t) +mgs_0\cos^2(\omega t)##
However, this is not true and the force is supposed to be ##C= 2m\omega^2 s_0 \sinh(\omega t)##, what am I doing wrong?
Last edited: