- #1
Lambda96
- 158
- 59
- Homework Statement
- Determine the point at which no force acts for general ##m_1## and ##m_2##.
- Relevant Equations
- none
Hi,
I had no problems calculating parts a and b, but I am having problems with task c
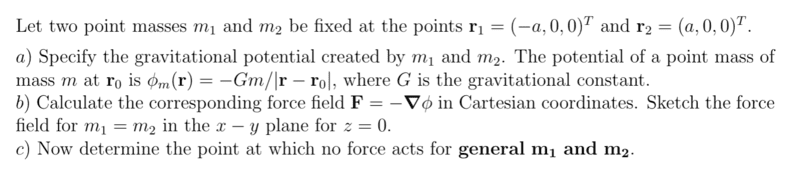
For ##F## I got the following, with ##\vec{r}= \left(\begin{array}{c} x \\\ y \\\ 0 \end{array}\right)## , ##\vec{r}_1= \left(\begin{array}{c} -a \\\ 0 \\\ 0 \end{array}\right)## and ##\vec{r}_2= \left(\begin{array}{c} a \\\ 0 \\\ 0 \end{array}\right)##
$$\vec{F}= \left(\begin{array}{c} \frac{Gm_1 (x-a)}{((x-a)^2+y^2)^{3/2}} + \frac{G m_2 (x+a)}{((x+a)^2+y^2)^{3/2}} \\ \frac{G m_1 y}{((a+x)^2+y^2)^{3/2}} + \frac{G m_2 y}{((x+a)^2+y^2)^{3/2}} \\ 0 \end{array}\right)$$
In order to determine the locations where the force is zero, I would have to solve the following system of equations
$$\frac{Gm_1 (x-a)}{((x-a)^2+y^2)^{3/2}} + \frac{G m_2 (x+a)}{((x+a)^2+y^2)^{3/2}}=0$$
$$\frac{G m_1 y}{((a+x)^2+y^2)^{3/2}} + \frac{G m_2 y}{((x+a)^2+y^2)^{3/2}}=0$$
But solving this system of equations would be extremely time-consuming and since the task gives few points, I assume that there is an easy way to determine the location, but unfortunately I don't know how?
I had no problems calculating parts a and b, but I am having problems with task c
For ##F## I got the following, with ##\vec{r}= \left(\begin{array}{c} x \\\ y \\\ 0 \end{array}\right)## , ##\vec{r}_1= \left(\begin{array}{c} -a \\\ 0 \\\ 0 \end{array}\right)## and ##\vec{r}_2= \left(\begin{array}{c} a \\\ 0 \\\ 0 \end{array}\right)##
$$\vec{F}= \left(\begin{array}{c} \frac{Gm_1 (x-a)}{((x-a)^2+y^2)^{3/2}} + \frac{G m_2 (x+a)}{((x+a)^2+y^2)^{3/2}} \\ \frac{G m_1 y}{((a+x)^2+y^2)^{3/2}} + \frac{G m_2 y}{((x+a)^2+y^2)^{3/2}} \\ 0 \end{array}\right)$$
In order to determine the locations where the force is zero, I would have to solve the following system of equations
$$\frac{Gm_1 (x-a)}{((x-a)^2+y^2)^{3/2}} + \frac{G m_2 (x+a)}{((x+a)^2+y^2)^{3/2}}=0$$
$$\frac{G m_1 y}{((a+x)^2+y^2)^{3/2}} + \frac{G m_2 y}{((x+a)^2+y^2)^{3/2}}=0$$
But solving this system of equations would be extremely time-consuming and since the task gives few points, I assume that there is an easy way to determine the location, but unfortunately I don't know how?