- #1
Mikeey aleex
- 7
- 0
hello every one
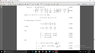
can one please construct for me left invariant vector field of so(3) rotational algebra using Euler angles ( coordinates ) by using the push-forward of left invariant vector field ? iv'e been searching for a method for over a month , but i did not find any well defined method for my case . i uploaded a pdf the give a direct formula for left invariant vector field , I've been trying to use push-forward method for one parameter subgroup , but i failed
can one please construct for me left invariant vector field of so(3) rotational algebra using Euler angles ( coordinates ) by using the push-forward of left invariant vector field ? iv'e been searching for a method for over a month , but i did not find any well defined method for my case . i uploaded a pdf the give a direct formula for left invariant vector field , I've been trying to use push-forward method for one parameter subgroup , but i failed