Converting Second Order ODE to Hypergeometric Function

[thatboi]

I believe it is the case that any linear second order ode with at most 3 regular singular points can be transformed into a hypergeometric function. I am trying to solve the following equation for a(x):

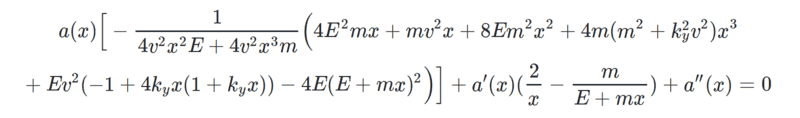
where E, m, v, k_{y} are all constants and I believe turning it into hypergeometric form will help me solve it. Any help would be appreciated!

 

[Paul Colby]

Have you located all the singular points? Just a quick look, $x=0$ and $x= -\frac{E}{m}$ look like candidates. What about at $x=\infty$? It would really help to reduce and simplify the constants.

 

[thatboi]

Have you located all the singular points? Just a quick look, $x=0$ and $x= -\frac{E}{m}$ look like candidates. What about at $x=\infty$? It would really help to reduce and simplify the constants.

It appears that $x=\infty$ is a singular point but it is not regular so I am not sure if we can use it here. Nevertheless it should still be possible to turn it into hypergeometric form right?
Also I am not sure what you mean by reducing and simplifying the constants here, I do not see anything that can be further cleaned up.

 

[Paul Colby]

Okay, so the hypergeometric equation is,

$z(1-z)\frac{d^2w}{dz^2} +[c-(a+b+1)z]\frac{dw}{dz} - abw = 0$

which has three regular singular points in the extended $z$-plane. These are at $z=0,1,\infty$. For starters you should transform your equations singular points to the same places. Two out out of three are already where they need to be. The last may be done by the change of variable,

$z = -\frac{m}{E}x$

if I've done things correctly. After this is done and you've multiplied through by the $z(1-z)$ factor, if you get the hypergeometric equation, you're done. If not, then your $a(x)$ isn't a hypergeometric function. That said, it may still be related to one with the right transformations.

 

[thatboi]

Right, but for my equation, x = $\infty$ isn't a regular singular point so are we still able to match it to that equation?

Okay, so the hypergeometric equation is,

$z(1-z)\frac{d^2w}{dz^2} +[c-(a+b+1)z]\frac{dw}{dz} - abw = 0$

which has three regular singular points in the extended $z$-plane. These are at $z=0,1,\infty$. For starters you should transform your equations singular points to the same places. Two out out of three are already where they need to be. The last may be done by the change of variable,

$z = -\frac{m}{E}x$

if I've done things correctly. After this is done and you've multiplied through by the $z(1-z)$ factor, if you get the hypergeometric equation, you're done. If not, then your $a(x)$ isn't a hypergeometric function. That said, it may still be related to one with the right transformations.

 

[Paul Colby]

I don't think it's likely. I'd have to do the work to find out. This is your question. If you transform the equation as suggested, what's the result?

 

[thatboi]

I don't think it's likely. I'd have to do the work to find out. This is your question. If you transform the equation as suggested, what's the result?

I get
$\begin{align} &z(1-z)\frac{d^2a}{dz^2}+(z-2)\frac{da}{dz} + \frac{1}{4m^2v^2z}(4E^2m^2+m^2v^2-4E^2m^2z+4Ek_{y}mv^2z+m^2v^2z\nonumber \\ &-4E^2m^2z^2-4E^2k_{y}^2v^2z^2+4E^2m^2z^3+4E^2k_{y}^2v^2z^3)a(z) = 0 \nonumber \end{align}$
which I guess is not the form we wanted.

 

[Paul Colby]

No, this is clearly not the hypergeometric equation. If I assume $E$ is energy, $m$ as mass, $v$ as velocity, the units between terms seems off. Oh, I'm also assuming this is an equation arising from a physics problem. I'd recheck your work.