Differentials in Multivariable Functions ....

[Math Amateur]

I am reading the book "Several Real Variables" by Shmuel Kantorovitz ... ...

I am currently focused on Chapter 2: Derivation ... ...

I need help with an aspect of Kantorovitz's Example 4 on page 66 ...

Kantorovitz's Example 4 on page 66 reads as follows:

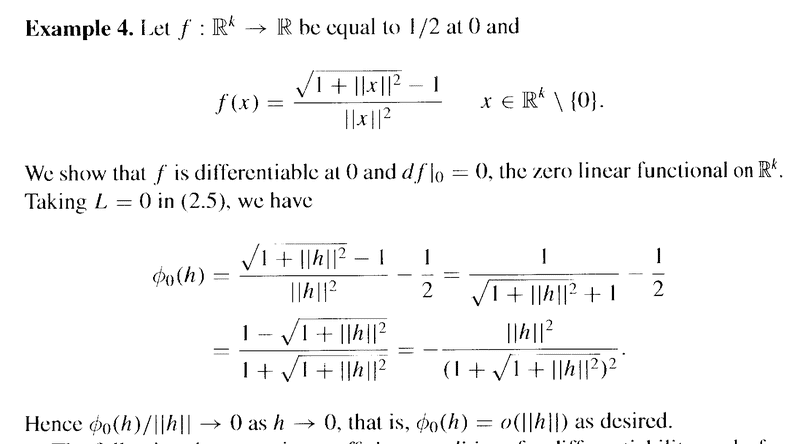
In the above example, Kantorovitz shows that$\phi_0 (h) = - \frac{ \| h \|^2 }{( 1 + \sqrt{ 1 + \| h \|^2 )}^2 }$Kantorovitz then declares that $\frac{ \phi_0 (h) }{ \| h \| } \rightarrow 0$ as $h \rightarrow 0$ ... ...Can someone please show me how to demonstrate rigorously that this is true ... that is that
$\frac{ \phi_0 (h) }{ \| h \| } \rightarrow 0$ as $h \rightarrow 0$ ... ...
Help will be much appreciated ...

Peter============================================================================================

***NOTE***

Readers of the above post may be helped by having access to Kantorovitz' Section on "The Differential" ... so I am providing the same ... as follows:

Hope that helps readers understand the context and notation of the above post ,,, ,,,

Peter

 

[Orodruin]

$\phi_0(h) = \mathcal O(h^2)$ implies that $\phi_0(h)/h=\mathcal O(h)$.

 

[Math Amateur]

$\phi_0(h) = \mathcal O(h^2)$ implies that $\phi_0(h)/h=\mathcal O(h)$.

Thanks for the reply Orodruin ...

BUT ... don't quite follow ... and do not see how to apply to the limit ...

Apologies if I'm being slow ...

PeterEdit: I do know that $O( \| h \| ) \Longrightarrow$ the ratios $\frac{ \mid \phi_0(h) \mid }{ \| h \| } ( h \neq 0 )$ are bounded ...

 

[fresh_42]

Thanks for the reply Orodruin ...

BUT ... don't quite follow ... and do not see how to apply to the limit ...

Apologies if I'm being slow ...

PeterEdit: I do know that $O( \| h \| ) \Longrightarrow$ the ratios $\frac{ \mid \phi_0(h) \mid }{ \| h \| } ( h \neq 0 )$ are bounded ...

You can think of $f(x)=O(g(x))$ as $f(x) \leq c\cdot g(x)$ for some constant $c$.

E.g. if $f(h)=c_1{h^2}+c_2{h^3}+c_3{h^4}+\ldots$ for small $h > 0$, then we can assume $h < 1$ and $h^2 > h^3 > h^4 >\ldots$ which means $f(h) \leq (\sum c_i) h^2$. So if the coefficients don't outnumber the behavior of ${h}$, i.e. if $\sum c_i = c$ is finite, then we get $f(h) \leq c \cdot h^2$ which we write as $f(h)=O(h^2).$ In this case however, we also have $\frac{1}{h}f(h) < c\cdot h$ and thus $\frac{f(h)}{h} =O(h)\,.$

A simple example for its usage is the matrix exponent. The question is about algorithms: How many multiplications of input variables are necessary to multiply two $(n \times n)$ matrices?

The ordinary way is to do it by $n^3$ multiplications. Improved algorithms can do it with $c \cdot n^\gamma$ multiplications (above some fixed $n$ where the improvement starts to be one) and $\gamma$ is somewhere above $2$ and of course below $3$ and $c$ a constant independent of $n$. The matrix algorithm then goes by $O(n^\gamma)$ essential multiplications. The infimum of these $\gamma$ is called the matrix exponent $\omega$, but this only as a side note. For short people say: matrix multiplication goes by $O(n^\omega)$. IIRC multiplication of $2 \times 2$ matrices which are usually done by eight multiplications can be done by only seven at the cost of additional additions, which shows $\omega < 3$.

The example above, $f(h)=O(h^2)$ means, that $f(h)$ doesn't grow faster than a constant multiple of $h^2\,.$
One of my favorite jokes is to write constants as $O(1)$.