Double integral Problem (with solution)

[DrWahoo]

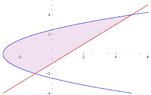
Evaluate (use attached figure for depiction) $ \iint_{R} \, xy \, dA $

where $R$ is the region bounded by the line
$y = x - 1$ and the parabola $y^2 = 2 x + 6$.

View attachment 7598

I will post solution in just a moment with a reply.

 

[DrWahoo]

Anyone want to attempt a solution or give some hints?

 

[MarkFL]

I would use horizontal strips, where:

$$\frac{y^2-6}{2}\le x\le y+1$$

And these strips run from:

$$-2\le y\le4$$

And so we obtain the iterated integral:

$$I=\int_{-2}^{4} y\int_{\Large{\frac{y^2-6}{2}}}^{y+1} x\,dx\,dy$$

I will leave it to a student to demonstrate:

$$I=36$$

 

[DrWahoo]

Thanks mark. I will give a little intuition as well and let a student come up with the result. This is just a reiteration of Marks work.

Based off of $\Bbb{R}$ pick to integrate with respect to $x$ first.
This would imply; that the boundaries of the region in the $x$ direction would be;
$x=\frac{(y^2)-6}{2} $ and $x=y+1$.

Now find the range, that is the range of values for $y$. In order to do this we need to find the $y$-coordinates in the points of the intersection between the following two curves;
$y=x-1$ and $y^2 =2x-6$.

Substituting $x=y+1$ into the second equation we obtain;
$y^2 =2(y+1)+6 $

Solve by factoring or quadratic formula to find the roots of the polynomial.
So we have $(y-4)(y+2)=0$ $\implies$ $y=4, y=-2$

Now try to set up the integrals to find the region requested;
I will give everyone a chance to set it up and or solve.

Thanks Mark.

I would use horizontal strips, where:

$$\frac{y^2-6}{2}\le x\le y+1$$

And these strips run from:

$$-2\le y\le4$$

And so we obtain the iterated integral:

$$I=\int_{-2}^{4} y\int_{\Large{\frac{y^2-6}{2}}}^{y+1} x\,dx\,dy$$

I will leave it to a student to demonstrate:

$$I=36$$

 

[HallsofIvy]

If you really want to use vertical strips, so that you are integrating with respect to x rather than y, you will need to break this into two integrals, one from -3 to -1, the other from -1 to 5.