Drawing Graphs: Concentric Circles & Straight Lines

[Raees]

Hi, how would I go about drawing these two graphs?

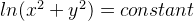
and

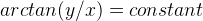The first one would be concentric circles with the centre at (0,0).
The second one would be straight lines through (0,0).

Is this correct?
Also, what happens at ln(0) = constant for the first graph and x = 0 for the second graph?

[Moderator's note: Moved from a technical forum and thus no template.]

 

[mfb]

Correct.

Also, what happens at ln(0) = constant for the first graph

That is not possible. x=y=0 is never a solution. Same for x=0 in the second case.

For "interesting" functions f(x)=constant usually means x has one or a somewhat special set of values for a given constant. If f is injective then it is equivalent to x=constant.

 

[HallsofIvy]

For the first one, $ln(x^2+ y^2)= constant$, taking the exponential of both sides, $x^2+ y^2= e^{constant}$. Yes, the graph of that is a circle with center at the origin and radius $\sqrt{e^{constant}}$.

For the second one, $arctan(y/x)= constant$, taking the tangent of both sides, $y/x= tan(constant)$ so $y= (tan(constant))x$. Since the tangent of a constant is also a constant, this is a straight line through the origin with slope tan(constant).

 

[Raees]

For the first one, $ln(x^2+ y^2)= constant$, taking the exponential of both sides, $x^2+ y^2= e^{constant}$. Yes, the graph of that is a circle with center at the origin and radius $\sqrt{e^{constant}}$.

For the second one, $arctan(y/x)= constant$, taking the tangent of both sides, $y/x= tan(constant)$ so $y= (tan(constant))x$. Since the tangent of a constant is also a constant, this is a straight line through the origin with slope tan(constant).

Thanks, that helps a lot!