Duistermaat & Kolk .... Vol II .... Proposition 6.1.2

[Math Amateur]

I am reading Multidimensional Real Analysis II (Integration) by J.J. Duistermaat and J.A.C. Kolk ... and am focused on Chapter 6: Integration ...

I need some help with the proof of Proposition 6.1.2 ...

Proposition 6.1.2 reads as follows:

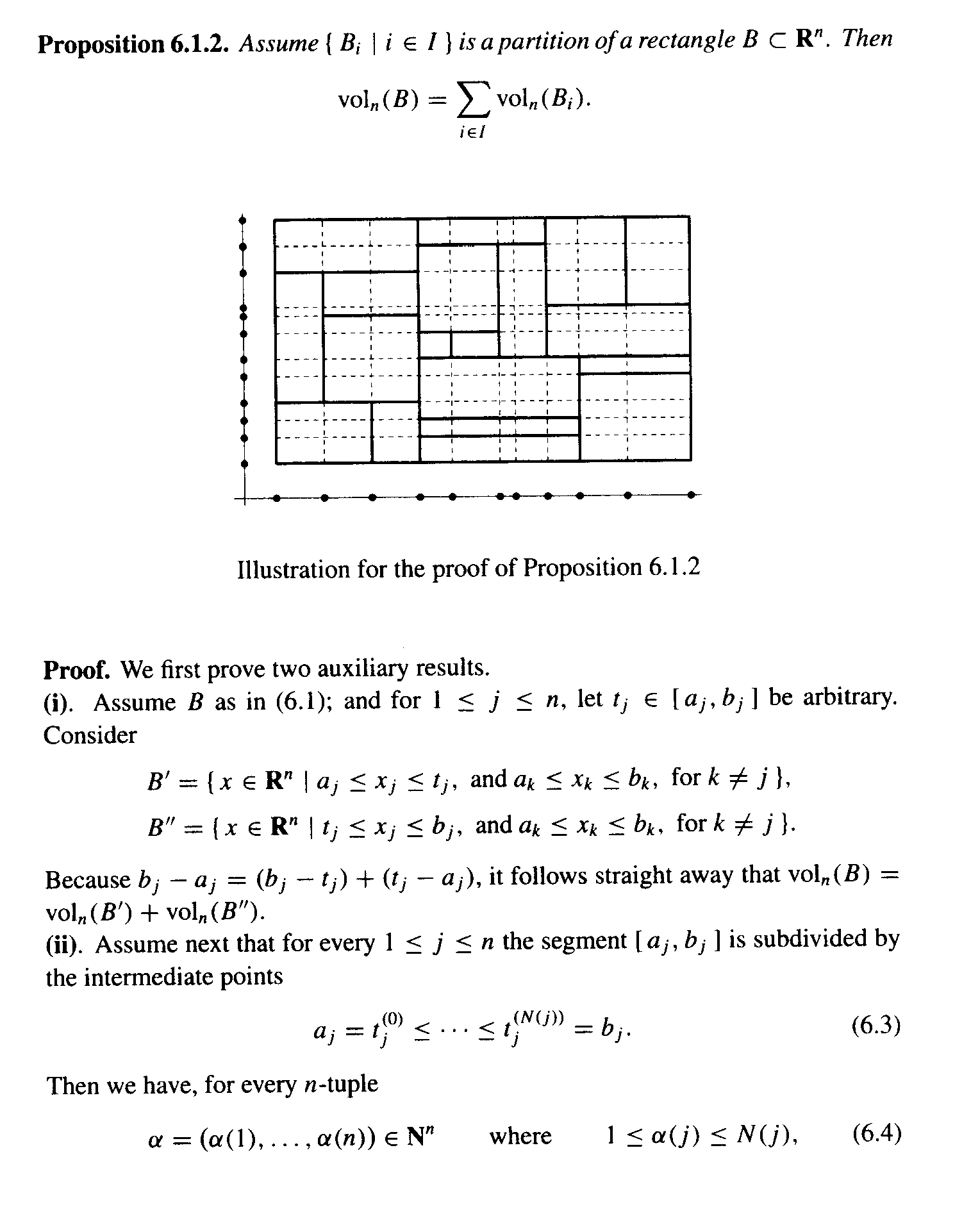
Definitions and text preliminary to the Proposition reads as follows:

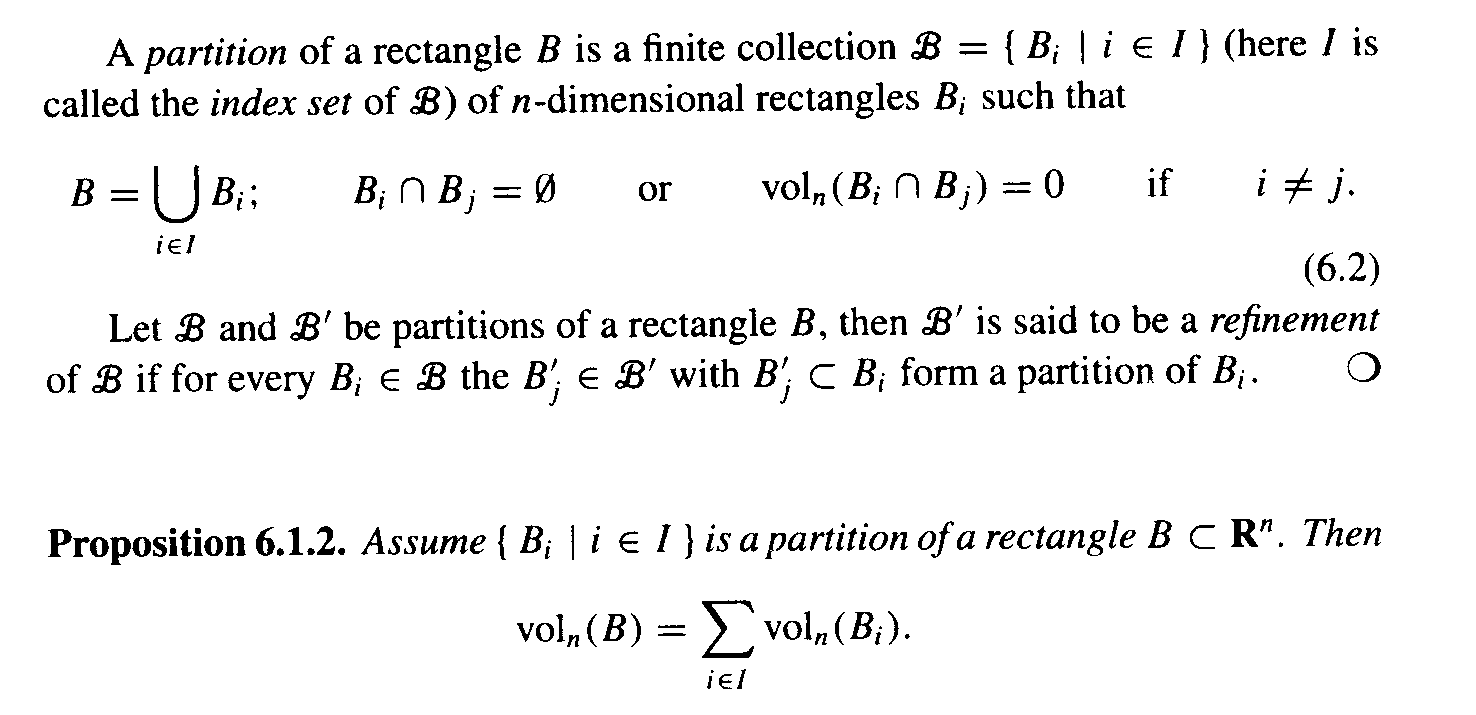
I am trying to write a detailed proof of the fact or assertion that

\(\displaystyle \text vol_n (B) =\text vol_n (B') + \text vol_n (B'') \) ... ... ... ... (*)

given their definitions as sets ... but have so far been able to formulate a proof ...

I hope someone can help ...

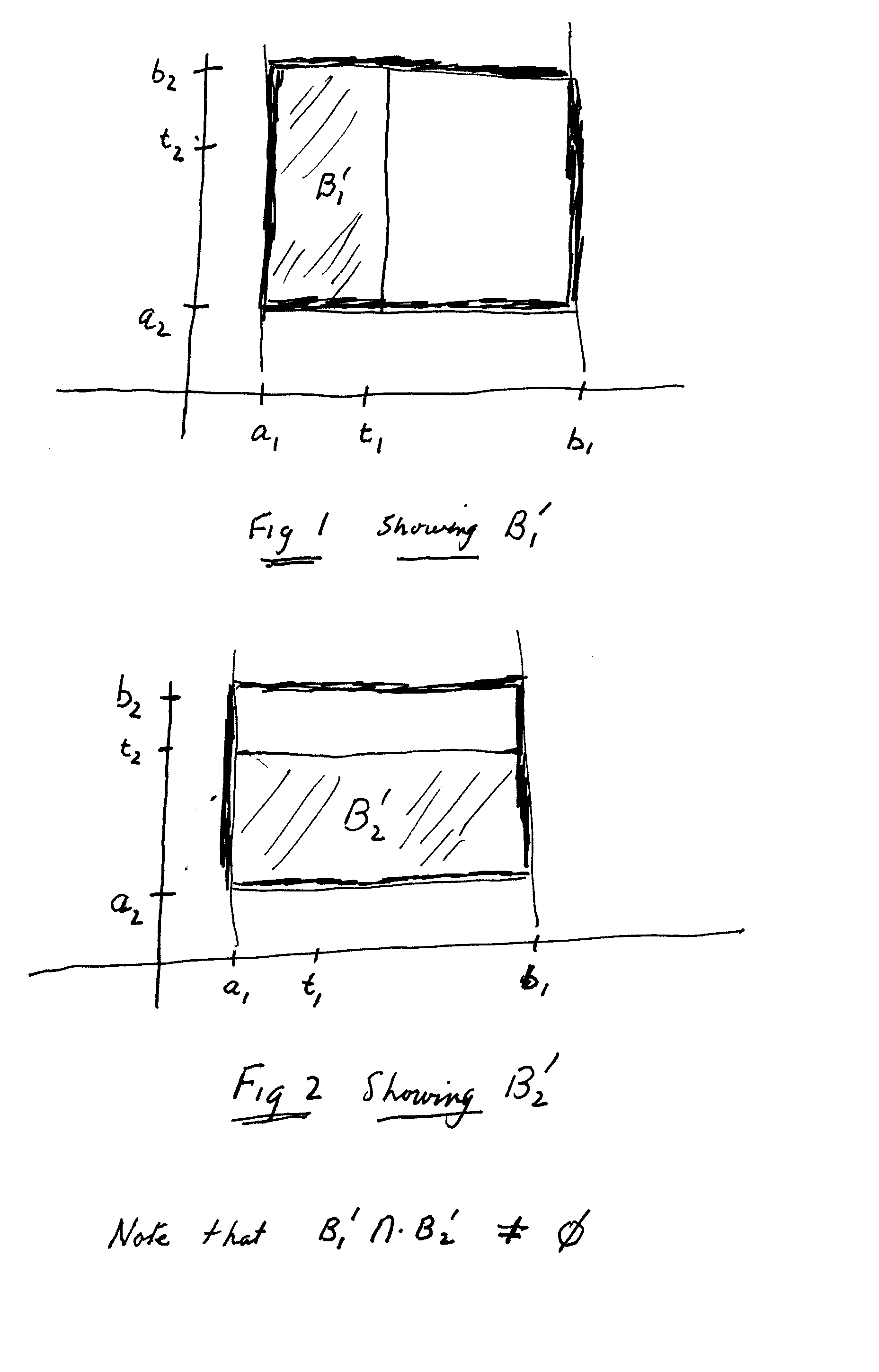
I am especially interested in tying or connecting the proof of (*) to the definitions of B' and B" as sets.To explicitly indicate my concerns I am presenting an example from $ \mathbb{R^2} $Let $ B' = \{ ( x_1, x_2 ) \in \mathbb{R^2} \; \; | \; \; a_1 \leq x_1 \leq t_1 \text{ and } a_2 \leq x_2 \leq b_2 \; \; ; \; \; \text{ and } a_2 \leq x_2 \leq t_2 \text{ and } a_1 \leq x_1 \leq b_1 \} $Thus B' is made up of two rectangles, viz.

$ B'_1 = \{ ( x_1, x_2 ) \in \mathbb{R^2} \; \; | \; \; a_1 \leq x_1 \leq t_1 \text{ and } a_2 \leq x_2 \leq b_2 \} $

and

$ B'_2 = \{ a_2 \leq x_2 \leq t_2 \text{ and } a_1 \leq x_1 \leq b_1 \} $

These two rectangles are depicted in Figures 1 and 2 below ...

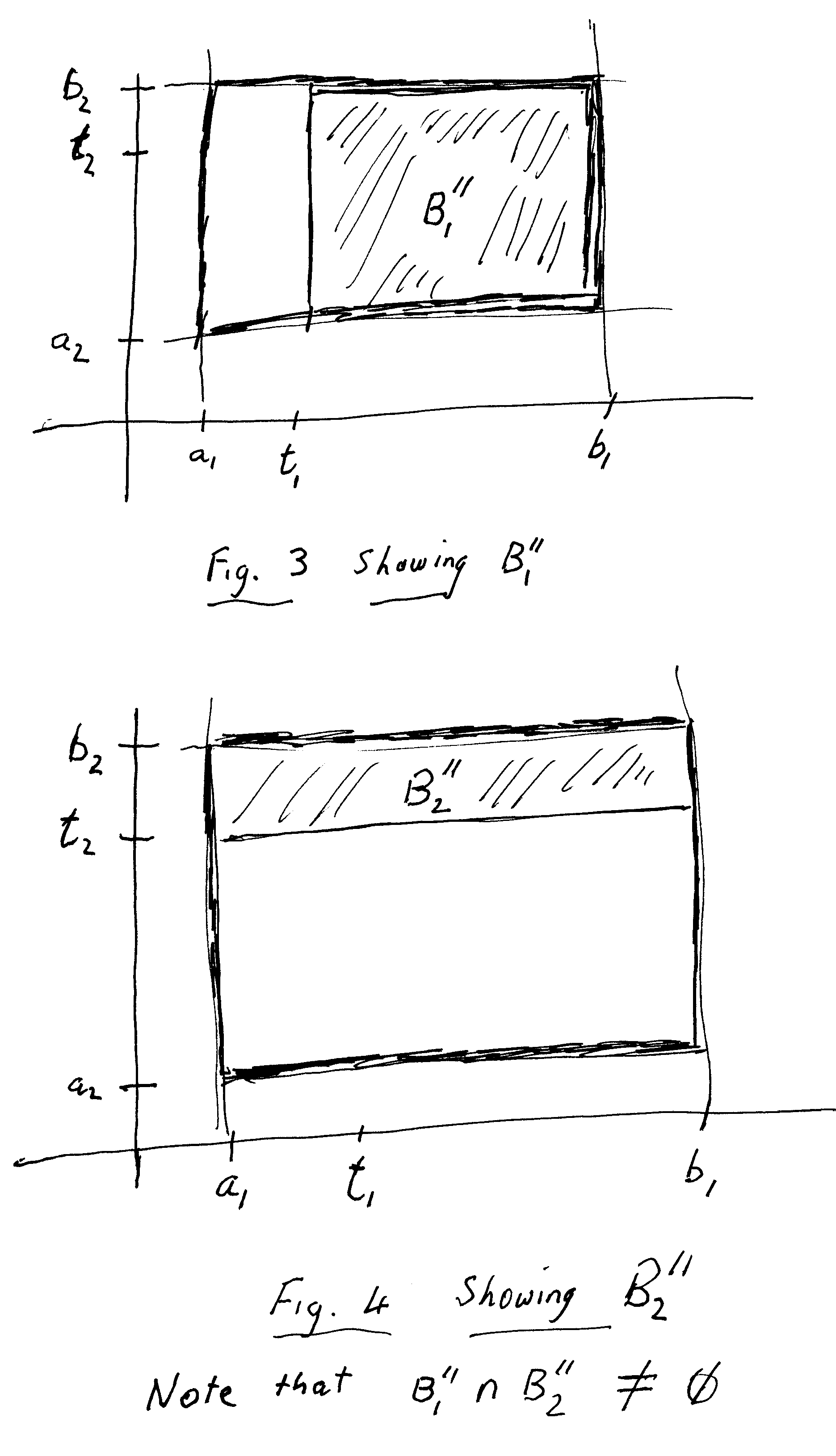
Now ... let $ B" = \{ ( x_1, x_2 ) \in \mathbb{R^2} \; \; | \; \; t_1 \leq x_1 \leq b_1 \text{ and } a_2 \leq x_2 \leq b_2 \; \; ; \; \; \text{ and } t_2 \leq x_2 \leq b_2 \text{ and } a_1 \leq x_1 \leq b_1 \} $Thus $ B" $ is made up of two rectangles, viz.

$ B"_1 = \{ ( x_1, x_2 ) \in \mathbb{R^2} \; \; | \; \; t_1 \leq x_1 \leq b_1 \text{ and } a_2 \leq x_2 \leq b_2 \} $

and$ B"_2 = \{ ( x_1, x_2 ) \in \mathbb{R^2} \; \; | \; \; t_2 \leq x_2 \leq b_2 \text{ and } a_1 \leq x_1 \leq b_1 \} $The above two rectangles $ B"_1 $ and $ B"_2 $ are depicted in Figures 3 and 4 below ...

Now ... my problem is this: I do not see how

$$\text vol_n (B) =\text vol_n (B') + \text vol_n (B'')$$ ... ... ... ... (*)

... that is I do not see how the volumes of $ B' $ and $ B" $ which together comprise the overlapping rectangles $ B'_1 , B'_2 , B"_1 \text{ and } B"_2 $ satisfy (*) ...Can someone explain how (*) can be true given my analysis above ... I must be making some errors ...NOTE: I know that (6.2) in the text in defining the conditions for a partition of a rectangle Duistermaat and Kolk write

$ B_i \cap B_j = \emptyset $ or $\text vol_n ( B_i \cap B_j ) = 0 $ if $ i \neq j $

... but this is prescriptively defining a partition of a rectangle $ B $ ... it does not, in my opinion, mean that we can overlook (put to zero) the overlaps or intersections in the rectangles $ B'_1 , B'_2, B"_1, \text{ and } B"_2 $ ...

Either way I cannot see how \(\displaystyle \text vol_n (B) =\text vol_n (B') + \text vol_n (B'') \) ... ... ... ... (*) arises from the union of the rectangles $ B'_1 , B'_2, B"_1, \text{ and } B"_2 $ ...Hope someone can explain and clarify this aspect of the proof of Proposition 6.1.2 ...

Peter

 

[jvicens]

,Thank you for your question and for providing such detailed background and examples. I can see why you are having trouble with the proof of Proposition 6.1.2, as it involves some tricky concepts and notations.

First, let's clarify the notation used in the proposition. The symbol $\text{vol}_n(A)$ is used to denote the $n$-dimensional volume (or measure) of a set $A$. In this context, $n$ refers to the dimension of the space in which the set is defined. So in your example, $n=2$ since we are working in $\mathbb{R}^2$. The sets $B'$ and $B''$ are defined as subsets of $\mathbb{R}^n$, so the proposition is essentially stating that the volume of $B$ is equal to the sum of the volumes of $B'$ and $B''$.

Now, let's take a closer look at the definition of $B'$ and $B''$. These sets are defined as unions of rectangles, where each rectangle is defined by a set of inequalities. For example, in your first rectangle, $B'_1$, the inequalities $a_1 \leq x_1 \leq t_1$ and $a_2 \leq x_2 \leq b_2$ define the boundaries of the rectangle. The same is true for the other rectangles in $B'$ and $B''$.

So when we take the union of these rectangles to form $B'$ and $B''$, we are essentially combining all the points that satisfy the inequalities defining each rectangle. This means that the points in the intersection of $B'$ and $B''$ will be counted twice when we calculate the volume of $B$, since they satisfy the inequalities defining both $B'$ and $B''$. This is why the proposition states that the volume of $B$ is equal to the sum of the volumes of $B'$ and $B''$ minus the volume of their intersection (which is being counted twice).

To illustrate this, let's look at your example in $\mathbb{R}^2$. In this case, $B'$ and $B''$ are made up of two rectangles each. When we take the union of these rectangles to form $B$, we are essentially combining the boundaries of all four rectangles. This means that the points in the intersection of the