- #1
- 2,168
- 193
Let us suppose we have an equation such that
$$N = \sum_{i=1}^N ix_i = x_1 + 2x_2 + 3x_3 + ...+Nx_N$$
and we also know that the solutions (i.e ##x_i##) ranges from ##\{0, N\}##.
For example, if ##N=4## we would have
$$x_1 + 2x_2 + 3x_3 + 4x_4 = 4$$
and ##x_1,x_2,x_3,x_4## will range from ##\{0, 4\}##. So the possible answers are
$$(x_1, x_2, x_3, x_4) = (0,0,0,1) / (1,0,1,0) / (0,2,0,0), (2, 1,0,0), (4,0,0,0)$$
Similarly for ##N=3## we would have
$$x_1 + 2x_2 + 3x_3 = 3$$
and ##x_1,x_2,x_3## will range from ##\{0, 3\}##. So the possible answers are
$$(x_1, x_2, x_3) = (0,0,1) / (1,1, 0) / (3,0,0)$$
I was studying Thermodynamics and this problem come to my mind which is actually used to describe the available states of the system (Note that this picture is about fermions, but my calculation works for the bosons. Nevertheless the idea is similar.)
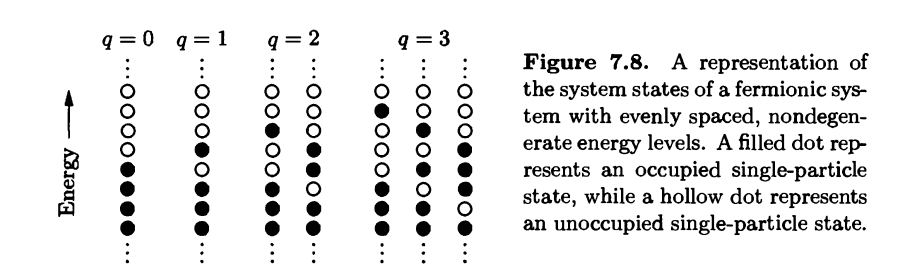
I neglected the ##q=0## and actually in my question ##q \equiv N##. I thought this could be a nice problem to computationally solve. The first solution come to mind is to create an array that contains all the possible answers of ##x_i## but that means we need ##N^N## elements which becomes quite hard to process for the computer. But that's indeed a silly solution.
More clever one is well for whatever number we put on the sum of the solutions cannot exceed ##N## (i.e ##x_1 + x_2 + ...+x_N \leq N## . So that might reduce the permutation number by a great amount. But I am also open to other ideas.
$$N = \sum_{i=1}^N ix_i = x_1 + 2x_2 + 3x_3 + ...+Nx_N$$
and we also know that the solutions (i.e ##x_i##) ranges from ##\{0, N\}##.
For example, if ##N=4## we would have
$$x_1 + 2x_2 + 3x_3 + 4x_4 = 4$$
and ##x_1,x_2,x_3,x_4## will range from ##\{0, 4\}##. So the possible answers are
$$(x_1, x_2, x_3, x_4) = (0,0,0,1) / (1,0,1,0) / (0,2,0,0), (2, 1,0,0), (4,0,0,0)$$
Similarly for ##N=3## we would have
$$x_1 + 2x_2 + 3x_3 = 3$$
and ##x_1,x_2,x_3## will range from ##\{0, 3\}##. So the possible answers are
$$(x_1, x_2, x_3) = (0,0,1) / (1,1, 0) / (3,0,0)$$
I was studying Thermodynamics and this problem come to my mind which is actually used to describe the available states of the system (Note that this picture is about fermions, but my calculation works for the bosons. Nevertheless the idea is similar.)
I neglected the ##q=0## and actually in my question ##q \equiv N##. I thought this could be a nice problem to computationally solve. The first solution come to mind is to create an array that contains all the possible answers of ##x_i## but that means we need ##N^N## elements which becomes quite hard to process for the computer. But that's indeed a silly solution.
More clever one is well for whatever number we put on the sum of the solutions cannot exceed ##N## (i.e ##x_1 + x_2 + ...+x_N \leq N## . So that might reduce the permutation number by a great amount. But I am also open to other ideas.
Last edited: