Effect of downward force on cantilevered object

[nezednemo]

TL;DR Summary

How much weight will it take to destabilize a table at the furthest most offset edge?

Hello,

a little about me: I’m a self trained craftsmen who has a deep hunger for knowledge. I have no formal training in physics or engineering. There are some principles I‘d like to understand better to improve my workflow. Please forgive any terminology faux pas, part of the issue I have in searching for these answers is I don’t have all the vocabulary down.

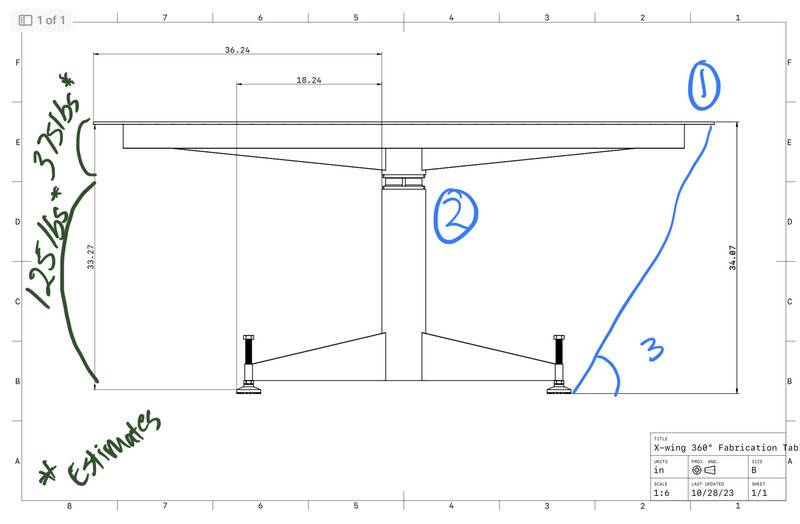
(1) I’d like to know how to calculate the force necessary to tip a cantilevered object like the table below.

(2) I’d like to have a better Understanding of how to calculate the combined center of mass of complex objects.

(3) I’d like to know if there are any rule of thumbs for angles of offsets. Obvious ≥ 90° is most stable, but is there an engineering principle that I could use to make. Faster calculations when designing products like this?

Thank you for your help

 

[jrmichler]

Starting with your question #1. The weight of the table times the distance from the center of mass (COM) to the farthest support point is the righting moment. Your feet have little swivels, so the distance is to the center of the foot as indicated in the sketch below. In this view, the table is symmetrical, so the horizontal location of the COM is at the center of the table. The vertical location of the COM needs to be calculated, but is not necessary for simple tipping calculations. Guessing at the exact dimensions, the righting moment is about $500 lbs * 19 inches = 9500 in-lbs$.

The tipping moment is the tipping force times the horizontal distance from the edge of the table to the nearest support foot. That distance is approximately 19" in your drawing. The tipping moment is thus the unknown force times 19 inches, and is equal to 9500 in-lbs. We calculate the unknown force by dividing 9500 by 19 inches, or $9500 in-lbs / 19 inches = 500 lbs$. The tipping force is equal to the weight of the table only because the two distances are equal.

Your question #2: Searching center of mass calculation will find some sites that explain it better than I can.

I do not understand your question #3.

 

[jack action]

View attachment IMG_0039-mod.webp​

@jrmichler was faster than me but I'll complete the answer.

I identified the lengths $T$, $B$ and $H$ on the drawing. Note that $T$ and $B$ should be measured from the center of the table where the center of gravity lies (correct position on both of our drawings).

The table will not tip if the moment created by the load $L$ is smaller than the moment created by the table weight $W$. The moment calculated about the pivot point where the reaction force $R$ is located gives:
$$L(T-B) < WB$$
Or:
$$L < W\frac{B}{T-B}$$
So when this is true, the table will not tip. (Basically what @jrmichler said.)

As to relate this to the angle at 3 - let's call it $\theta$:

Basic geometry states that:
$$\tan \theta = \frac{H}{T-B}$$
Or:
$$T-B = \frac{H}{\tan \theta}$$Putting that in our original equation:
$$L < W\frac{B}{H}\tan \theta$$
Or:
$$\theta > \tan^{-1}\left(\frac{L}{W}\frac{H}{B}\right)$$
If this is true, the table will not tip. For example, if you want the table to be able to hold a 1000 lb load $L$, you have:
$$\theta > \tan^{-1}\left(\frac{1000}{500}\frac{34.07}{18.24}\right)$$
$$\theta > 75°$$
So if the angle is greater than $75°$, the table should not tip.

 

[nezednemo]

This was very helpful.

I think I got what I was looking for in question 3 which was a rule of thumb that could help with quick estimates in the design process-

If the furthest support is half the distance to the furthest offset edge than the weight to tip the structure at the offset edge is roughly equal to the weight of the structure.

did I get this right? Would additional height/higher COM effect this significantly?

 

[jack action]

If the furthest support is half the distance to the furthest offset edge than the weight to tip the structure at the offset edge is roughly equal to the weight of the structure.

Yes.

did I get this right? Would additional height/higher COM effect this significantly?

No. Height would only play a role with horizontal forces.

 

[Baluncore]

The tipping moment is the tipping force times the horizontal distance from the edge of the table to the nearest support foot.

To be more precise, it is not the nearest support foot that counts, but the innermost point on the "hinge line" between the nearest two feet, and the outermost edge of the table beyond that "hinge line".
It can be solved from a plan view of the table, but not from the side elevation.

 

[nezednemo]

To be more precise, it is not the nearest support foot that counts, but the innermost point on the "hinge line" between the nearest two feet, and the outermost edge of the table beyond that "hinge line".
It can be solved from a plan view of the table, but not from the side elevation.

 

[Baluncore]

I want a plan, then I get two elevations and an oblique, all with different numbers to the OP.
a = from CofM to edge of table.
b = from CofM to hinge line on floor.
c = a - b = cantilever.
Wcritical = mass * b / c
Wside = 500 * 11.81 / ( 23.81 - 11.81 ) = 492 on the side edge.
Wend = 500 * 19.50 / ( 39.00 - 19.50 ) = 500 on end edge.

 

[nezednemo]

 

[Baluncore]

The 1:2 ratio in the plan, suggests that any edge can support an additional purely vertical load, equal to the weight of the table, before it tips. As you approach that limit, small side forces can become critical and should not be ignored.

I see the feet have now become 3" diameter discs. If they have swivels, or rest on thick carpet, you should ignore the foot diameter and assume the load is applied at the centre point, on the hinge-line.