Electric and Magnetic field acting on an electron

[Joseph Rolls]

Homework Statement

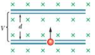
In the figure, an electron of mass m, charge − e, and low (negligible) speed enters the region between two plates of potential difference V and plate separation d, initially headed directly toward the top plate. A uniform magnetic field of magnitude B is normal to the plane of the figure. Find the minimum value of B such that the electron will not strike the top plate.

Homework Equations

F=qE=Vq/d
F=qvBsin(θ)
F=ma
a=v^2/r

The Attempt at a Solution

Assuming that the electric field accelerates the electron towards the top plate, as the electron accelerates, v will increase so the magnetic force acting on it increases, which acts on the electron in the direction according to the RH rule.
I'm not sure how to incorporate all these equations together, as v is not constant and neither is the direction which the magnetic force acts on the electron, neither is the path circular or the acceleration constant.
Do I need to form some sort of integral regarding the change in v with d and integrate, or how else do i attack this problem? Or am I missing some fundamental concept?

 

[BvU]

Hello joseph,

which acts on the electron in the direction according to the RH rule

All well and good so far. Which direction is that specifically ? What does that mean for the radius of the trajectory ?

 

[Chandra Prayaga]

Is the upper plate at higher or lower potential relative to the lower plate?

 

[Delta2]

This can be solved by solving a system of two coupled linear differential equations. Are you being asked to solve it without solving at all differential equations?

 

[Joseph Rolls]

Hello joseph,

All well and good so far. Which direction is that specifically ? What does that mean for the radius of the trajectory ?

Well initially it is to the right, but as the electron changes direction the magnetic force direction will also change, swinging around until it points down as the electron just nearly touches the plate, it means the radius will be curved but it won't be a circular trajectory because of the force from the charged plates…?

Is the upper plate at higher or lower potential relative to the lower plate?

Well I assume the upper plate is at a higher potential else the question is sort of pointless, it doesn't actually specify though.

This can be solved by solving a system of two coupled linear differential equations. Are you being asked to solve it without solving at all differential equations?

The question doesn't specify but I guess that'd nearly be the only way to solve it would it?
Would it look something like ma=Ftotal=md^2x/dt^2=qV/d-qBcosθdx/dt where θ is the angle between the x-axis and the tangent of the electron's path. and we're only interested in the j component of the electron's path. or is this completely the wrong idea?

Thanks for your help everyone

 

[BvU]

Well initially it is to the right, but as the electron changes direction the magnetic force direction will also change, swinging around until it points down as the electron just nearly touches the plate, it means the radius will be curved but it won't be a circular trajectory because of the force from the charged plates…?

My point is that you should calculate the radius and see what comes out -- who knows some effects counteract each other ( The B part of the Lorentz force $\vec v \times \vec B\,$ increases with $|\vec v|$ -- I didn't work this out in detail -- after all I'm just a helper )

 

[Delta2]

Would it look something like ma=Ftotal=md^2x/dt^2=qV/d-qBcosθdx/dt where θ is the angle between the x-axis and the tangent of the electron's path. and we're only interested in the j component of the electron's path. or is this completely the wrong idea?

Thanks for your help everyone

Well you could make the system of the ordinary differential equations, either by using the velocity $v$ and the angle $\theta$ as unknowns, or the velocities $v_x$, $v_y$ as unknowns. The differential equation you wrote is not entirely correct but even if it was, the critical point is that the $\theta$ angle is not constant but depends on time, therefore you have two unknowns, so you need two equations to solve for them.
The vector equation for the total force is

$$m_e\frac{d\vec{v}}{dt}=q\frac{V}{d}\vec{j}+q\vec{v}\times \vec{B} (1)$$

Now I believe the best way is to substitute $\vec{v}=v_x\vec{i}+v_y\vec{j}$ and then from the vector equation (1) you ll get two equations one for the $\vec{i}$ component and one for the $\vec{j}$ component. (Be careful how you will evaluate the cross product $(v_x\vec{i}+v_y\vec{j})\times B\vec{k}$).

 

[Joseph Rolls]

Well you could make the system of the ordinary differential equations, either by using the velocity $v$ and the angle $\theta$ as unknowns, or the velocities $v_x$, $v_y$ as unknowns. The differential equation you wrote is not entirely correct but even if it was, the critical point is that the $\theta$ angle is not constant but depends on time, therefore you have two unknowns, so you need two equations to solve for them.
The vector equation for the total force is

$$m_e\frac{d\vec{v}}{dt}=q\frac{V}{d}\vec{j}+q\vec{v}\times \vec{B} (1)$$

Now I believe the best way is to substitute $\vec{v}=v_x\vec{i}+v_y\vec{j}$ and then from the vector equation (1) you ll get two equations one for the $\vec{i}$ component and one for the $\vec{j}$ component. (Be careful how you will evaluate the cross product $(v_x\vec{i}+v_y\vec{j})\times B\vec{k}$).

Ok…so i subbed in $\vec{v}=v_x\vec{i}+v_y\vec{j}$ and got $$m_e\frac{d\v_x\vec{i}}{dt}=q\frac{V}{d}\vec{j}+q\vec{v}\times \vec{B} $$ and $$m_e\frac{d\v_y\vec{j}}{dt}=q\vec{j}(frac{V}{d}+\vec{v_y}\times \vec{B}) $$ and said that for the electron to just not touch the top plate, the force in the $\vec{j}$ direction must be 0 and therefore $$(frac{V}{d}+\vec{v_y}\times \vec{B})=0 $$ or as $v_y$ is perpendicular to B and at that point |$v_y$|=v, we have V/d+vB=0, or B=-V/vd.

v can be found as the increase in kinetic energy is qV, so v=root(2qV/m).

therefore Bmin=root(mV/2e)/d

is this correct?

apologies for the dodgy syntax, I'm not really sure how to use the vector language correctly in this post

 

[Delta2]

Ok…so i subbed in $\vec{v}=v_x\vec{i}+v_y\vec{j}$ and got $$m_e\frac{dv_x\vec{i}}{dt}=q\frac{V}{d}\vec{j}+q\vec{v}\times \vec{B} $$ and $$m_e\frac{dv_y\vec{j}}{dt}=q\vec{j}(\frac{V}{d}+\vec{v_y}\times \vec{B}) $$ and said that for the electron to just not touch the top plate, the force in the $\vec{j}$ direction must be 0 and therefore $$(\frac{V}{d}+\vec{v_y}\times \vec{B})=0 $$ or as $v_y$ is perpendicular to B and at that point |$v_y$|=v, we have V/d+vB=0, or B=-V/vd.

v can be found as the increase in kinetic energy is qV, so v=root(2qV/m).

therefore Bmin=root(mV/2e)/d

is this correct?

apologies for the dodgy syntax, I'm not really sure how to use the vector language correctly in this post

You don't seem to calculate the cross product terms correctly. It is $$(v_x\vec{i}+v_y\vec{j})\times B\vec{k}=v_xB\vec{i}\times\vec{k}+v_yB\vec{j}\times\vec{k}=-v_xB\vec{j}+v_yB\vec{i}$$
So the differential equations after we split the vector equation to i and j components are
$$m_e\frac{dv_x}{dt}=qv_yB$$
$$m_e\frac{dv_y}{dt}=-qv_xB+q\frac{V}{d}$$
These two are coupled linear ODEs, before we proceed we have to decouple them so we get one equation that has only $v_x$ appearing and another that has only $v_y$.

The rest of the calculation you perform are not correct cause as you can see from the second equation above, $v_y$ is not only affected by the electric field force $q\frac{V}{d}$, but also from the magnetic field force component $-qv_xB$.

 

[Delta2]

Hmm, what we did so far is not wrong, however I just thought an easier way of solving this, without getting into the trouble of setting up and solving differential equations.
We have to think in energy-work terms. The magnetic field performs no work on the particle, hence it doesn't increase its kinetic energy.
The increase in the kinetic energy can come only from the electric field.

We want the particle just to touch the upper plate , so when it reaches the upper plate it should be $v_y=0$ and $v_x$ will be determined by conservation of energy . Its kinetic energy at the upper plate will be $\frac{1}{2}m(v_x^2+v_y^2)=\frac{1}{2}mv_x^2$. Its kinetic energy at the bottom plate is zero.

What energy equation can you make if you apply conservation of energy for the bottom and top positions?

From that equation you should be able to determine $v_x$. Then make a force balance equation in the y-axis at the top position of the particle, so that the total force in the y-axis is zero. From this equation you ll determine the minimum value of magnetic field required.

I know this solutions seems counter intuitive at start, since we accept that the increase of $v_x$ comes from the electric field which is perpendicular to the x-axis, but what happens is that the electric field increases $v_y$ and the magnetic field transfers energy from $v_y$ to $v_x$ component.

 

[Joseph Rolls]

You don't seem to calculate the cross product terms correctly. It is $$(v_x\vec{i}+v_y\vec{j})\times B\vec{k}=v_xB\vec{i}\times\vec{k}+v_yB\vec{j}\times\vec{k}=-v_xB\vec{j}+v_yB\vec{i}$$
So the differential equations after we split the vector equation to i and j components are
$$m_e\frac{dv_x}{dt}=qv_yB$$
$$m_e\frac{dv_y}{dt}=-qv_xB+q\frac{V}{d}$$
These two are coupled linear ODEs, before we proceed we have to decouple them so we get one equation that has only $v_x$ appearing and another that has only $v_y$.

The rest of the calculation you perform are not correct cause as you can see from the second equation above, $v_y$ is not only affected by the electric field force $q\frac{V}{d}$, but also from the magnetic field force component $-qv_xB$.

oh yep, i forgot that minus sign, i wondered why i had an extra one later one.

what you've said in your second post is what i said before but maybe i didn't make it clear.
kinetic energy increase is the decrease in potential energy from the electric field which is qV, and so we have

0.5mv^2=qV, => v=sqrt(2qV/m)

then as you said we have the force in the $\vec{j}$ direction = 0, which means
-qvB+qV/d=0
=>B=V/dv=V/d*sqrt(2qV/m)=sqrt(mV/2q)

Thanks heaps for your help!

 

[Delta2]

oh yep, i forgot that minus sign, i wondered why i had an extra one later one.

what you've said in your second post is what i said before but maybe i didn't make it clear.
kinetic energy increase is the decrease in potential energy from the electric field which is qV, and so we have

0.5mv^2=qV, => v=sqrt(2qV/m)

then as you said we have the force in the $\vec{j}$ direction = 0, which means
-qvB+qV/d=0
=>B=V/dv=V/d*sqrt(2qV/m)=sqrt(mV/2q)

Thanks heaps for your help!

Ok well now I understand this is correct (I think you forgot a d in the denominator in the final result btw) , just to emphasize that the velocity v in your calculation is $v_x$ not $v_y$.

 

[Charles Link]

@Delta² (and @Joseph Rolls ) Independently I just worked the problem and got the same coupled differential equations you did in post 9. The solution of them is rather straightforward. First, it's an inhomogeneous second order equation for $v_x$ with a simple particular solution, and the solution to the homogeneous part is a simple $v_x=A cos(\omega t)+B \sin(\omega t)$, with the $B \sin(\omega t)$ getting eliminated because $\dot{v}_x=0$ at $t=0$. The $A$ is calculated with the particular solution and the condition that $v_x=0$ at $t=0$.$\\$ It is then straightforward to compute $v_y$ and also to integrate $s=\int\limits_{0}^{t} v_y(t) \, dt$. This is a function that takes the form $s=C(1-\cos(\alpha t))$ and you simply need to make $2C <d$. $\\$ Additional item: I get (Edit) $B_o=\frac{1}{d} \sqrt{\frac{2Vm}{q}}$. Looking at your solution, the acceleration and force in the $\hat{j}$ direction will not be zero at this point (the highest point). The particle is instantaneously in a circular motion at this point, (Edit: At least one can anticipate a non-zero downward acceleration) so it is[Edit:][likely to be] accelerating downward. I think that is the reason the solutions are not in agreement. At this highest point $B$ needs to be strong enough to make the net force be in the minus y direction, and will be more than the value you calculated to make the y-force zero. The equations of motion show that this value of $B$ is such that it makes $qv_xB = \frac{2qV}{d}$. $\\$ I think this problem might require a computation of the equations of motion with the coupled equations. It was a clever attempt at a short-cut, but I think it is incorrect.

 

[Delta2]

hmm, @Charles Link are you sure about your result for $B_o$, it doesn't depend on d, shouldn't the distance d play a role?
And yes as you say it was a clever attempt for a shortcut ( I was inspired by the other problem with the pulleys and bodies m and M) to use an energy method that might give the result without the trouble of ODEs.

Not sure I think your result about $B_o$ isn't dimensionally correct, there must be a d somewhere.

 

[Charles Link]

$V=E d$. @Delta² I haven't carefully checked all of the algebra, but it is simply a factor of 2 larger than what @Joseph Rolls calculated using your method of post 9, and I believe it is correct. Suggestion: Try working the coupled equations and see if your result agrees with mine.

 

[Delta2]

@Charles Link Ok I ll check the solutions to ODEs myself but I think somewhere you miscalculated a factor of 2.

And the value of $B_o$ at post 13 really is $B_o=\frac{1}{d}\sqrt\frac{2Vm}{q}$, that is it has the 1/d in front right?

 

[Charles Link]

And the value of BoBoB_o at post 13 really is Bo=1d√2VmqBo=1d2VmqB_o=\frac{1}{d}\sqrt\frac{2Vm}{q}, that is it has the 1/d in front right?

Yes. Thank you. I see where I hurried my very last step: Yes, there should be a $\frac{1}{d}$ there. Let me also correct it above.

 

[Delta2]

Well I solved for $v_y$ and found it to be

$$v_y=\frac{V}{Bd}\sin({\frac{Bq}{m}t})$$.

Integrating we get

$$s_y=\frac{Vm}{B^2dq}(1-\cos({\frac{Bq}{m}t}))$$

This means that the maximum value that $s_y$ can have is $2\frac{Vm}{B^2dq}<d$ so we get Charles result from this.

 

[Charles Link]

@Delta² I am very pleased that you got the same thing I did. $\\$ When you throw a ball up, the acceleration is non-zero at the top of the arc even though the y-velocity is zero. With this one, it conceivably could have had a zero y-acceleration at the top of the arc, but the equations of motion have shown it doesn't. $\\$ We should eventually post the solution for $v_x$ as well, but I would really like to let the OP @Joseph Rolls also work the problem, rather than simply giving him the complete solution. This one is a good exercise in solving an inhomogeneous second order linear differential equation. It is really quite a neat problem, and I hadn't seen anything previously quite like it.

 

[Delta2]

Yes @Charles Link it turns out that it has vertical acceleration pointing downwards , at the top point. What's the catch with the clever shortcut of the energy approach? We just computed a lower bound for the $B_{min}$ there and not the actual $B_{min}$ (which turns to be 2x that lower bound).

The catch is that we say that the particle when it reaches the top plate must have $v_y=0$. But in order for this to happen it turns out (from the differential equations) that the magnetic field must have exactly a value of $\frac{1}{d}\sqrt\frac{2Vm}{q}$ which turns to be exactly double of the lower bound we calculated with the energy approach. If that value was the same as the lower bound we computed with the energy approach, then the energy approach would be correct, but it isn't . So some times clever shortcuts are not so clever or accurate, have to do the hard work with the differential equation setup and solving.

 

[Joseph Rolls]

First, it's an inhomogeneous second order equation for vxvx v_x

Sorry, this is probably a really stupid question, but how is it a second order equation?

 

[Charles Link]

If you look at post 9, you can see $v_y=\frac{m}{qB } \frac{dv_x}{dt}$. Substitute this into the $dv_y$ equation, the result is: $\\$ $\frac{m^2}{qB}(\frac{d^2v_x}{dt^2})+qBv_x=\frac{qV}{d}$. $\\$ The solution of this involves a particular solution to the inhomogeneous equation along with a homogeneous solution. I'd be happy to show you the details, but see first if you might be able to solve it.$\\$ For initial conditions, we have $v_x=0$ at $t=0$, and also because $v_y=0$ at $t=0$, by the first equation, that also makes $\frac{dv_x}{dt}=0$ at $t=0$. $\\$ Once you solve for $v_x$ , you then solve for $v_y$ using the first equation. Finally, to get y-distance $s$, that is given by $s=\int\limits_{0}^{t} v_y \, dt$.

 

[Joseph Rolls]

First, it's an inhomogeneous second order equation for vxvx v_x with a simple particular solution, and the solution to the homogeneous part is a simple vx=Acos(ωt)+Bsin(ωt)vx=Acos(ωt)+Bsin⁡(ωt) v_x=A cos(\omega t)+B \sin(\omega t) , with the Bsin(ωt)Bsin⁡(ωt) B \sin(\omega t) getting eliminated because ˙vx=0v˙x=0 \dot{v}_x=0 at t=0t=0 t=0 . The AA A is calculated with the particular solution and the condition that vx=0vx=0 v_x=0 at t=0t=0 t=0 .

ok so i got $v_x$ = Acos(qbt/m)+Csin(qbt/m) for the homogeneous solution, but if $v_x$ = 0, when t=0, then doesn't that imply A=0 so we eliminate the Acos(qbt/m) from our equation instead of the sin? although i think this is wrong because this leads me to get $v_x$ = V/Bd and that hence $v_y$ = 0 which isn't right. what am i stuffing up here?

 

[Charles Link]

ok so i got $v_x$ = Acos(qbt/m)+Csin(qbt/m) for the homogeneous solution, but if $v_x$ = 0, when t=0, then doesn't that imply A=0 so we eliminate the Acos(qbt/m) from our equation instead of the sin? although i think this is wrong because this leads me to get $v_x$ = V/Bd and that hence $v_y$ = 0 which isn't right. what am i stuffing up here?

You need to include the particular solution $v_{xp}$, i.e. the solution to the (complete) inhomogeneous differential equation. For this case it is very simple: $v_{xp}=\frac{V}{bd}$, (a constant, independent of the time $t$), so that $v_x(t)=A \cos(\frac{qbt}{m})+B \sin(\frac{qbt}{m}) +\frac{V}{bd}$, ( where because of the coefficient $B$, I followed your convention to use $b$ for the magnetic field). $\\$ $A=-\frac{V}{bd}$, and $B =0$ when you put in the boundary conditions. The $A$ is obtained from $v_x=0$ at $t=0$, and the $B=0$ results because $\frac{dv_x}{dt}=0$ at $t=0$.

 

[Joseph Rolls]

You need to include the particular solution $v_{xp}$, i.e. the solution to the complete inhomogeneous differential equation. For this case it is very simple: $v_{xp}=\frac{V}{bd}$, (a constant, independent of the time $t$), so that $v_x(t)=A \cos(\frac{qbt}{m})+B \sin(\frac{qbt}{m}) +\frac{V}{bd}$, ( where because of the coefficient $B$, I followed your convention to use $b$ for the magnetic field). $\\$ $A=-\frac{V}{bd}$, and $B =0$ when you put in the boundary conditions. The $A$ is obtained from $v_x=0$ at t=0 $and the$ B=0 $follows because$ \frac{dv_x}{dt}=0 $at$ t=0 ##.

oh yeahhh of course, that was stupid of me, I found the particular solution $v_{xp}=\frac{V}{bd}$, but forgot to include it.
Awesome, I get the same solutions for vx, vy and s as you and delta^2 too now.
That being vx=-V/(Bd)cos(Bqt/m)+V/Bd and the other two as stated.
Thanks heaps again for all your help.

 

[Charles Link]

oh yeahhh of course, that was stupid of me, I found the particular solution $v_{xp}=\frac{V}{bd}$, but forgot to include it.
Awesome, I get the same solutions for vx, vy and s as you and delta^2 too now.
That being vx=-V/(Bd)cos(Bqt/m) and the other two as stated.
Thanks heaps again for all your help.

$v_x=\frac{V}{Bd}(1-\cos(\frac{qBt}{m}) )$, and $v_y=\frac{m}{qB} (\frac{dv_x}{dt})=\frac{V}{Bd} \sin(\frac{qBt}{m})$. $\\$ Edit: Notice also, $v_x$ is always greater than or equal to zero. As the particle cycles back and forth in the y direction, there is a drift to the right (the +x direction).