Engine Finite Heat Release Model (With Heat Transfer) Help

[Jason Louison]

Hello Physics Forum Users! I have an annoying situation with the Finite Heat Release Equation used to simulate combustion and expansion processes in an internal combustion engine. The equation is as follows:

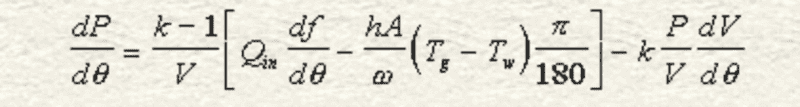
Nomenclature:

P = Cylinder Pressure (kPa)
θ = Crank Angle (Deg)
k = Specific Heat Ratio
V = Cylinder Volume (m³)
Qin = Heat Input (J)
ƒ = mass fraction burned (Wiebe Function, %)
h = heat transfer coefficient (W/m²-K)
A = Cylinder Wall Surface Area (m²)
ω = Engine Speed (rad/s..?)
T_g = Cylinder Gas Temperature (K)
T_w = Cylinder Wall Temperature (K)
I do not know why π/180 is there, maybe someone can explain it to me?
of course, df/dθ and dV/dθ are rate of change equations for Cylinder Volume and Mass Fraction Burned.

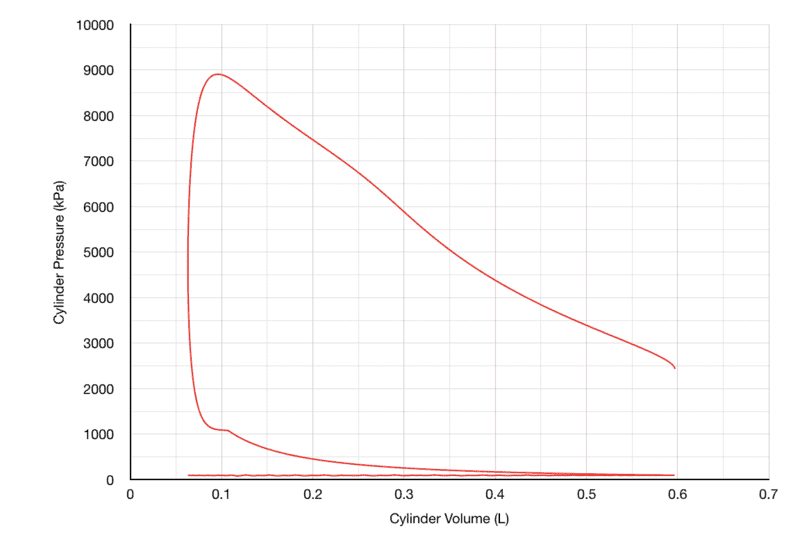
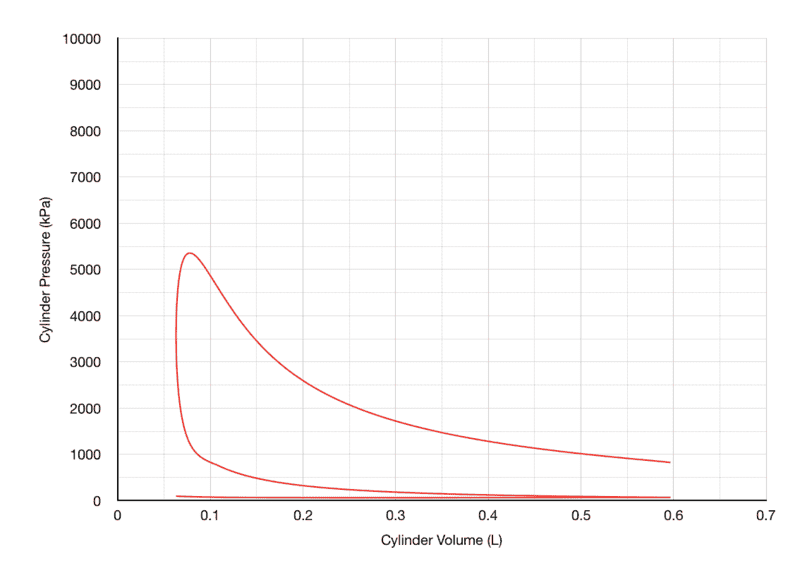
So, here's where things get a little weird. To obtain cylinder pressure, I Calculate dP/dθ, then multiply it by (1/720), and then add it to the initial pressure, p(θ-1). Yeah I know, it doesn't make much sense, in fact that right there may be my biggest mistake. But If I were to multiply dP/dθ by dθ, my data would be very inconclusive, as dθ for every cell is 1. multiplying the equation by 1 and adding it to the the initial pressure generates very weird data, and, unfortunately, some errors as well. The second issue is that when the engine speed is low, (Below 6500 RPM), The expansion pressure section is very obscure looking:

1000 RPM (Ignition Timing=-28° BTC): Way too much area under curve

8500 RPM (Ignition Timing=-28° BTC): Normal-looking curve

Sources used:
https://www.engr.colostate.edu/~allan/engines.html

I have looked everywhere to try and find out what I am doing wrong, but I found nothing. :(

 

[DonKiwi]

Hi, Jason. I just joined this group and spotted an unexpected opportunity to be slightly useful before any chance arises of being a pest later.
I notice that the parameters which you listed are in S.I. units (System Internationale to someone of your ancestry, and thankfully a standard used by a very high proportion of the known universe) with the exceptions of 1): Pressure (It should be the base unit of Pascals) and 2): Crank Angle in Degrees.
Given that Crank Angle is practicably entered as Degrees, the factor of Π/180 converts Degrees to Radians which is the S.I. unit of angle.
The Radian is considered dimensionless, making the units of angular velocity; ω to be [1/seconds] ~ (such that, for example, Torque * angular velocity = Power.
[Newton*metres] x [1/second] = [Joules / second] =[Watts] ).
Perhaps the value in [kPa] which you may have used, together with your mentioned application of the factor: (1 / 720) have caused your unexpected result.
It seems that the "1/720" is a second (partial) adjustment of units to that already made by the "Π/180" (Your question mark after engine speed units suggests doubt).
You might also have to audit further because of the "%" cited in the Mass Fraction. Disrupting factors of 1000 ( [kPa/Pa] ) & (1 / 720 ) & 0.01 ( [ % ] / Ratio ) will certainly produce "very weird data".

 

[Jason Louison]

Hi, Jason. I just joined this group and spotted an unexpected opportunity to be slightly useful before any chance arises of being a pest later.
I notice that the parameters which you listed are in S.I. units (System Internationale to someone of your ancestry, and thankfully a standard used by a very high proportion of the known universe) with the exceptions of 1): Pressure (It should be the base unit of Pascals) and 2): Crank Angle in Degrees.
Given that Crank Angle is practicably entered as Degrees, the factor of Π/180 converts Degrees to Radians which is the S.I. unit of angle.
The Radian is considered dimensionless, making the units of angular velocity; ω to be [1/seconds] ~ (such that, for example, Torque * angular velocity = Power.
[Newton*metres] x [1/second] = [Joules / second] =[Watts] ).
Perhaps the value in [kPa] which you may have used, together with your mentioned application of the factor: (1 / 720) have caused your unexpected result.
It seems that the "1/720" is a second (partial) adjustment of units to that already made by the "Π/180" (Your question mark after engine speed units suggests doubt).
You might also have to audit further because of the "%" cited in the Mass Fraction. Disrupting factors of 1000 ( [kPa/Pa] ) & (1 / 720 ) & 0.01 ( [ % ] / Ratio ) will certainly produce "very weird data".

Haha, I know very well that MFB has to be actual percent (1.00 instead of 100). That would result in an astronomical error xD. I have been playing around with the Heat loss term a bit, I have yet to come to a conclusion as to what I am doing wrong, but I'm getting there!