Entries in a direction cosine matrix as derivatives

[maxhersch]

This is a somewhat vague question that stems from the entries in a directional cosine matrix and I believe the answer will either be much simpler or much more complicated than I expect.

So consider the transformation of an arbitrary vector, v, in ℝ² from one frame f = {x₁ , x₂} to a primed frame
f' = {x'₁ , x'₂} which is related to the non-primed frame by a rotation of angle γ.

The transformation matrix will look like this:

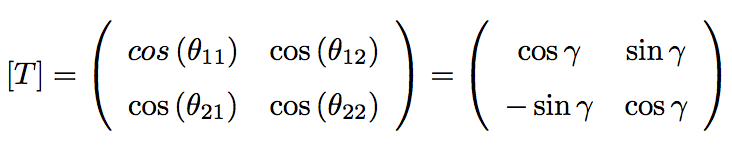
So this matrix can be derived from some simple trigonometric identities, specifically
$$ cos( \frac {\pi}{2} + \gamma) = -sin(\gamma) $$ and $$ cos(\frac {\pi}{2} - \gamma) = sin(\gamma) $$
So my question is perhaps more related to these identities than the matrix. Nonetheless, why are the entries in the 2nd column of the transformation matrix equivalent to the derivative of the entries in the 1st column? Is there some intuitive explanation, perhaps related to the trig identities? Regardless of how simple or complex the reasoning may be, I would appreciate some insight just for the sake of my curiosity. Thanks.

 

[StoneTemplePython]

The transformation matrix will look like this:

So this matrix can be derived from some simple trigonometric identities, specifically
$$ cos( \frac {\pi}{2} + \gamma) = -sin(\gamma) $$ and $$ cos(\frac {\pi}{2} - \gamma) = sin(\gamma) $$
So my question is perhaps more related to these identities than the matrix

This may not be quite what you are looking for, but I'd point out that a decent chunk of what we call trig identities comes from symbol manipulation of Taylor Series of sine and cosine. Put differently, people use calculus to get these identities.

The idea, is that, if you are constructing your rotation matrices correctly, a lot of these trig identities must follow from simple matrix multiplication, which I find to be more intuitive, especially when people draw nice pictures to go along. Take a look at this video:

https://www.lem.ma/web/#/content/VQ7wysLCIGIM0Hd7

He shows how $cos(\alpha +\beta) = cos(\alpha) cos(\beta) - sin(\alpha)sin(\beta)$ (plus a similar identity for $sin(\alpha + \beta)$) must follow if you've set up your rotation matrices correctly.

A different, perhaps less satisfying take, is to consider the converse -- if we set up the rotation matrix in another way, we'd be contradicting well know trig identities.

Hopefully this is close to what you are asking in your question.