- #1
chwala
Gold Member
- 2,650
- 351
- Homework Statement
- Write down an irrational number, ##n## where ##31<n< 32## [1mark]
- Relevant Equations
- past international exam paper- Numbers
I just came across this question and the ms indicates,
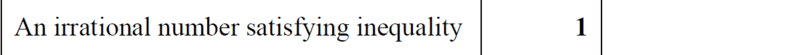
Would ##31.5## be correct? ...i think it is rational as it can be expressed as ##31.5 = \dfrac{63}{2}##.
Would ##31.5## be correct? ...i think it is rational as it can be expressed as ##31.5 = \dfrac{63}{2}##.