Find cosine series: Period 4 for f(x)

[evinda]

Hello!

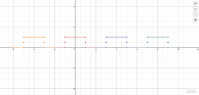
I want to find the Fourier series for the given function $f$:

$f(x)=\left\{\begin{matrix}
1, & 0<x<1,\\
0, & 1<x<2
\end{matrix}\right.$

-> cosine series, period 4

I also want to find the graph of the function to which the series converges , for three periods and then make some comparisons with 2 other examples.In order to find the cosine Fourier series, do we have to find the even extension of $f$? If so, will this be equal to $0$ for $-1<x<0$ and to $1$ for $-2<x<-1$ ?

But then the extension wouldn't be $4$-periodic? Would it? (Worried)

 

[I like Serena]

Hey evinda! (Smile)

In order to find the cosine Fourier series, do we have to find the even extension of $f$?

Yes.

If so, will this be equal to $0$ for $-1<x<0$ and to $1$ for $-2<x<-1$ ?

The even extension should have $f(x)=f(-x)$.
Would that be the case? (Wondering)

But then the extension wouldn't be $4$-periodic? Would it?

To be $4$-periodic, we should also extend the function so that $f(x+4)=f(x)$ for all $x\in \mathbb R$. (Thinking)

 

[evinda]

The following function is the even extension of $f$, isn't it?

$g(x)=\left\{\begin{matrix}
1 & , 0<x<1\\
0 & ,1 <x<2\\
1 & , -1<x<0\\
0 & , -2<x<1
\end{matrix}\right.$

Do we include the points $0,1$ and $1,2$ at the interval at which $g$ is defined?

 

[I like Serena]

The following function is the even extension of $f$, isn't it?

$g(x)=\left\{\begin{matrix}
1 & , 0<x<1\\
0 & ,1 <x<2\\
1 & , -1<x<0\\
0 & , -2<x<1
\end{matrix}\right.$

Yep.

Do we include the points $0,1$ and $1,2$ at the interval at which $g$ is defined?

Do we have to?
Let's not and see what happens. (Smirk)

 

[evinda]

Do we have to?
Let's not and see what happens. (Smirk)

Ok... The coefficients of the cosine Fourier series are given by the following formulas:

$$a_n=\frac{2}{L} \int_0^L f(x) \cos{\frac{n \pi x}{L}} dx, n=0,1,2, \dots \\ b_n=0, n=1,2, \dots$$

So in our case $a_0= \int_0^2 g(x) dx=1$ and $a_n=\int_0^2 g(x) \cos{\frac{n \pi x}{2}} dx=\int_0^1 \cos{\frac{n \pi x}{2}} dx=\frac{2}{n \pi} \sin{\frac{n \pi }{2}}$.

So the Fourier series is of the following form, right?

$$f(x)=\frac{1}{2}+ \frac{2}{\pi} \sum_{n=1}^{\infty} \frac{\sin{\frac{n \pi }{2}}}{n} $$

 

[I like Serena]

Ok... The coefficients of the cosine Fourier series are given by the following formulas:

$$a_n=\frac{2}{L} \int_0^L f(x) \cos{\frac{n \pi x}{L}} dx, n=0,1,2, \dots \\ b_n=0, n=1,2, \dots$$

Since we have a couple of undefined points, is this integral well defined? (Wondering)

So in our case $a_0= \int_0^2 g(x) dx=1$ and $a_n=\int_0^2 g(x) \cos{\frac{n \pi x}{2}} dx=\int_0^1 \cos{\frac{n \pi x}{2}} dx=\frac{2}{n \pi} \sin{\frac{n \pi }{2}}$.

So the Fourier series is of the following form, right?

$$f(x)=\frac{1}{2}+ \frac{2}{\pi} \sum_{n=1}^{\infty} \frac{\sin{\frac{n \pi }{2}}}{n} $$

What happened to $x$ in the right hand side? (Worried)

 

[evinda]

Since we have a couple of undefined points, is this integral well defined? (Wondering)

I thought so since the integral doesn't depend on each point seperately. Am I wrong?

What happened to $x$ in the right hand side? (Worried)

Oh sorry, I meant $g(x)=\frac{1}{2}+\frac{2}{ \pi}\sum_{n=1}^{\infty} \frac{\sin{\frac{n \pi}{2}}}{n} \sin{\frac{n \pi x}{2}}$.

Is this right? (Thinking)

 

[I like Serena]

I thought so since the integral doesn't depend on each point seperately. Am I wrong?

That depends on which integral we use.
The Riemann integral is defined for a function on the whole closed interval, but the Rieman-Stieltjes integral does not seem to have that limitation. The Lesbesgue integral certainly doesn't.
Either way, we can arbitrarily extend the function to be defined in every point, but it won't have any effect on the integral.
The definition of the cosine series here only requires that the function is integrable, but doesn't say which integral.
Anyway, since it simply does not matter for the end result, there is little point in worrying about it.

Oh sorry, I meant $g(x)=\frac{1}{2}+\frac{2}{ \pi}\sum_{n=1}^{\infty} \frac{\sin{\frac{n \pi}{2}}}{n} \sin{\frac{n \pi x}{2}}$.

Is this right? (Thinking)

Weren't we creating a cosine series? (Wondering)

 

[evinda]

That depends on which integral we use.
The Riemann integral is defined for a function on the whole closed interval, but the Rieman-Stieltjes integral does not seem to have that limitation. The Lesbesgue integral certainly doesn't.
Either way, we can arbitrarily extend the function to be defined in every point, but it won't have any effect on the integral.
The definition of the cosine series here only requires that the function is integrable, but doesn't say which integral.
Anyway, since it simply does not matter for the end result, there is little point in worrying about it.

Neither in the notes I am reading it says which integral we use... (Thinking)

Weren't we creating a cosine series? (Wondering)

Oh sorry, again a typo... (Tmi)

I meant that we get this:

$$g(x)=\frac{1}{2}+\frac{2}{ \pi}\sum_{n=1}^{\infty} \frac{\sin{\frac{n \pi}{2}}}{n} \cos{\frac{n \pi x}{2}}$$

Is this right? (Thinking)

 

[I like Serena]

I meant that we get this:

$$g(x)=\frac{1}{2}+\frac{2}{ \pi}\sum_{n=1}^{\infty} \frac{\sin{\frac{n \pi}{2}}}{n} \cos{\frac{n \pi x}{2}}$$

Is this right? (Thinking)

Yep. (Nod)

 

[evinda]

Yep. (Nod)

And we get that $g(x)=\frac{1}{2}+\frac{2}{\pi} \sum_{n=1}^{\infty} \frac{(-1)^{\frac{n-1}{2}}}{2n-1} \cos{\frac{(2n-1) \pi x}{2}}$. Right?

I saw at the solutions that it stands $f(x)=\frac{1}{2}+ \frac{2}{\pi}\sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{2n-1} \cos{\frac{(2n-1) \pi x}{2}} $. Isn't the power of $-1$ wrong? (Thinking)

 

[I like Serena]

And we get that $g(x)=\frac{1}{2}+\frac{2}{\pi} \sum_{n=1}^{\infty} \frac{(-1)^{\frac{n-1}{2}}}{2n-1} \cos{\frac{(2n-1) \pi x}{2}}$. Right?

I saw at the solutions that it stands $f(x)=\frac{1}{2}+ \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{2n-1} \cos{\frac{(2n-1) \pi x}{2}} $. Isn't the power of $-1$ wrong? (Thinking)

Let's take a look at the first couple of terms in both cases... (Thinking)

\begin{aligned}\frac{1}{2}+\frac{2}{\pi} \sum_{n=1}^{\infty} \frac{(-1)^{\frac{n-1}{2}}}{2n-1} \cos{\frac{(2n-1) \pi x}{2}}
&= \frac 12 + \frac 2\pi \left(
\frac{(-1)^{\frac{1-1}{2}}}{2\cdot 1-1} \cos{\frac{(2\cdot 1-1) \pi x}{2}}
+ \frac{(-1)^{\frac{2-1}{2}}}{2\cdot 2-1} \cos{\frac{(2\cdot 2-1) \pi x}{2}} + ... \right) \\
&= \frac 12 + \frac 2\pi \left(
\cos{\frac{\pi x}{2}}
+ \frac{\sqrt{-1}}{3} \cos{\frac{3 \pi x}{2}} + ... \right)
\end{aligned}
That can't be right can it? (Wondering)
We shouldn't have imaginary numbers in there.
And shouldn't the $\cos$ occurrences be of the form $\cos(k\pi x)$ with $k$ an integer?

\begin{aligned}\frac{1}{2}+ \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{2n-1} \cos{\frac{(2n-1) \pi x}{2}}
&= \frac 12 + \left( \frac{(-1)^{1-1}}{2\cdot 1-1} \cos{\frac{(2\cdot 1-1) \pi x}{2}}
+ \frac{(-1)^{2-1}}{2\cdot 2-1} \cos{\frac{(2\cdot 2-1) \pi x}{2}} + ... \right) \\
&= \frac 12 + \left( \cos{\frac{\pi x}{2}}
- \frac 13 \cos{\frac{3 \pi x}{2}} + ... \right)
\end{aligned}
At least the coefficients are real, but this doesn't look right either.
The $\cos$ occurrences are not of the form $\cos(k\pi x)$ with $k$ an integer. (Worried)

 

[evinda]

Let's take a look at the first couple of terms in both cases... (Thinking)

\begin{aligned}\frac{1}{2}+\frac{2}{\pi} \sum_{n=1}^{\infty} \frac{(-1)^{\frac{n-1}{2}}}{2n-1} \cos{\frac{(2n-1) \pi x}{2}}
&= \frac 12 + \frac 2\pi \left(
\frac{(-1)^{\frac{1-1}{2}}}{2\cdot 1-1} \cos{\frac{(2\cdot 1-1) \pi x}{2}}
+ \frac{(-1)^{\frac{2-1}{2}}}{2\cdot 2-1} \cos{\frac{(2\cdot 2-1) \pi x}{2}} + ... \right) \\
&= \frac 12 + \frac 2\pi \left(
\cos{\frac{\pi x}{2}}
+ \frac{\sqrt{-1}}{3} \cos{\frac{3 \pi x}{2}} + ... \right)
\end{aligned}
That can't be right can it? (Wondering)
We shouldn't have imaginary numbers in there.
And shouldn't the $\cos$ occurrences be of the form $\cos(k\pi x)$ with $k$ an integer?

\begin{aligned}\frac{1}{2}+ \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{2n-1} \cos{\frac{(2n-1) \pi x}{2}}
&= \frac 12 + \left( \frac{(-1)^{1-1}}{2\cdot 1-1} \cos{\frac{(2\cdot 1-1) \pi x}{2}}
+ \frac{(-1)^{2-1}}{2\cdot 2-1} \cos{\frac{(2\cdot 2-1) \pi x}{2}} + ... \right) \\
&= \frac 12 + \left( \cos{\frac{\pi x}{2}}
- \frac 13 \cos{\frac{3 \pi x}{2}} + ... \right)
\end{aligned}
At least the coefficients are real, but this doesn't look right either.
The $\cos$ occurrences are not of the form $\cos(k\pi x)$ with $k$ an integer. (Worried)

It says that the solution is $f(x)=\frac{1}{2}+\frac{2}{\pi} \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{2n-1} \cos{\frac{(2n-1) \pi x}{2}}$... (Blush)

But how do we get the $(-1)^{n-1}$ ?

The $\cos$ occurences should be of the form $\cos{\frac{n \pi x}{L}}$ where $L$ is $2$ in this case. Or not? (Thinking)

 

[evinda]

Ah it is as follows:$$g(x)=\frac{1}{2}+\frac{2}{ \pi}\sum_{n=1}^{\infty} \frac{\sin{\frac{n \pi}{2}}}{n} \cos{\frac{n \pi x}{2}}$$

If $n$ is even, then $\sin{\frac{n \pi}{2}}=0$.

If $n$ is odd then $n=2k-1$ for some $k \in \mathbb{Z}$.

Then $\sin{\frac{n \pi}{2}}=\sin{\frac{(2k-1)\pi}{2}}=\sin{\left(k \pi-\frac{\pi}{2}\right)}=\sin{k \pi} \cos(-\frac{\pi}{2})+\cos{k \pi} \sin{\left(-\frac{\pi}{2}\right)}=-\cos{k \pi}=(-1)^{k-1}$.

So, $g(x)=\frac{1}{2}+\frac{2}{ \pi}\sum_{k=1}^{\infty} (-1)^{k-1} \frac{1}{2k-1} \cos{\frac{(2k-1) \pi x}{2}}$The graph of the function to which the Fourier series converges is the following, right?View attachment 6579

 

[I like Serena]

Yep. All correct. (Nod)

 

[evinda]

Nice... And I should also make comparisons with the following two problems:

1. Let $f(x)=\left\{\begin{matrix}
0 & , -L <x<0,\\
L & ,0<x<L
\end{matrix}\right.$, and suppose that $f$ is defined at the external of this interval so that $f(x+2L)=f(x)$ for each $x$. Then the Fourier series of $f$ is $f(x)=\frac{L}{2}+ \frac{2L}{ \pi} \sum_{n=1}^{\infty} \frac{\sin{\left( (2n-1) \frac{\pi x}{L}\right)}}{2n-1}$.

and

2. Find the Fourier series of the extended function $f(x)=\left\{\begin{matrix}
0 & , - \pi \leq x<-\frac{\pi}{2},\\
1 & , -\frac{\pi}{2} \leq x< \frac{\pi}{2}\\
0 & , \frac{\pi}{2} \leq x< \pi
\end{matrix}\right.$

I have found that the Fourier series is the following:

$f(x)=\frac{1}{2}+ \frac{2}{ \pi} \sum_{n=1}^{\infty} \frac{1}{2n-1} (-1)^{n-1} \cos{(2n-1)x}$.What observations could we make? (Thinking)

 

[I like Serena]

Can we graph them? (Wondering)

The formulas are very similar, (1) with a sine instead of a cosine, and no alternating $-1$.
And (2) with only a different factor inside the $\cos$.
The graph for (1) looks pretty different though, and for (2) the effect is a scaling along the x-axis.