- #1
steveZ
- 21
- 12
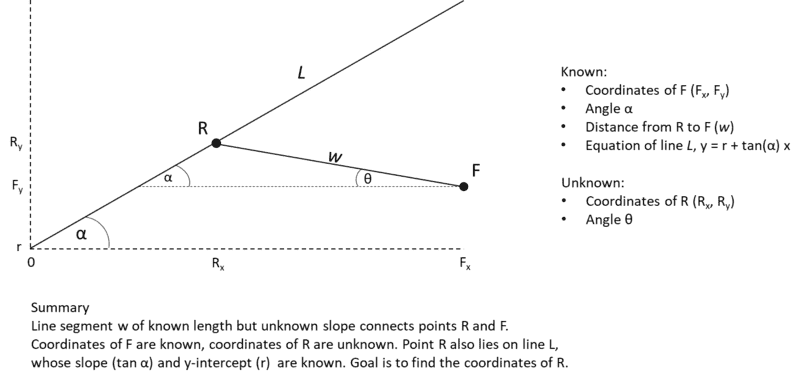
The image below should explain the problem and the constraints. Basically, I know the location of one point (F) in 2-D space (Cartesian coordinates). A line segment (w) of known length connects this point to another point (R). The coordinates of R are unknown; however, it is known to lie on a line (L), the slope and y-intercept of which are known (tanα and r). My intuition is that this should be solvable and not all that complicated. The slope of segment w is unknown, but there should only be one angle that allows a segment of that length to exactly reach line L. But I cannot figure it out so I am appealing to the community.