Goochie1234's questions at Yahoo Answers regarding polar/rectangular conversions

[MarkFL]

Here are the questions:

Trigonometry: polar coordinates help?

Need some help here please

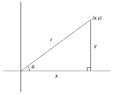
1. the rectangular point are given. Find the polar coordinates (R, θ) of this point with θ expressed in radiant. Let R>0 and -2pi< θ<2pi

2. the letters X and Y represent rectangular coordinates, write the given equation using polar coordinates (r,θ)

A. 2r^2 sin (2θ)=1
B.2r^2 cos (2θ)=1
C. 4r^2 sin (2θ)=1
D. 4r^2 cos(2θ)=1

3.the letters X and Y represent rectangular coordinates, write the given equation using polar coordinates (r,θ)

A. r= 5/ cosθ + sin θ
B. r=5
C. r^2=5/ cosθ + sin θ
D. r^2=5

4. the letters r and θ represent polar coordinates. write the given equation using the rectangular coordinates (x,y)

r=8

0=?

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello goochie1234,

The key to working these problems are the following relations:

\(\displaystyle (x,y)=(r\cos(\theta),r\sin(\theta))\)

\(\displaystyle x^2+y^2=r^2\)

The first is obtained directly from the definitions of the sine and cosine functions, while the second is a result of the Pythagorean theorem. Consider the following sketch:

View attachment 954

We have the point $(x,y)$ to which we draw a line segment from the origin, and lalbe its length as $r$. From the point we drop a vertical line segment to the $x$-axis (at the point $(x,0)$ and its length must be $y$.

Using the definition of the sine function on this right triangle, we find:

\(\displaystyle \sin(\theta)=\frac{\text{opposite}}{\text{hypotenuse}}=\frac{y}{r}\)

and so we find:

(1) \(\displaystyle y=r\sin(\theta)\)

Likewise, using the definition of the cosine function on this right triangle, we find:

\(\displaystyle \sin(\theta)=\frac{\text{adjacent}}{\text{hypotenuse}}=\frac{x}{r}\)

and so we find:

(2) \(\displaystyle x=r\cos(\theta)\)

We may also observe that:

\(\displaystyle \frac{y}{x}=\frac{r\sin(\theta)}{r\cos(\theta)}= \tan(\theta)\)

Hence:

(3) \(\displaystyle \theta=\tan^{-1}\left(\frac{y}{x} \right)\)

Note: If $x=0$, then \(\displaystyle \theta=\pm\frac{\pi}{2}\).

By Pythagoras, we can then easily see:

(4) \(\displaystyle x^2+y^2=r^2\)

So, having these relationships, we can now answer the questions.

1. The rectangular point $(x,y)$ is given. Find the polar coordinates $(r,\theta)$ of this point with $\theta$ expressed in radians. Let $0<r$ and $-2\pi<\theta<2\pi$.

From (3) and (4), we may then state:

\(\displaystyle r=\sqrt{x^2+y^2}\)

\(\displaystyle \theta=\tan^{-1}\left(\frac{y}{x} \right)\)

2.) The letters $x$ and $y$ represent rectangular coordinates. Write the given equations using polar coordinates $(r,\theta)$.

A. \(\displaystyle 2r^2\sin(2\theta)=1\)

I would use the double-angle identity for sine \(\displaystyle \sin(2\alpha)=2\sin(\alpha)\cos(\alpha)\) to rewrite the equation as:

\(\displaystyle 4r^2\sin(\theta)\cos(\theta)=1\)

We may rewrite this as:

\(\displaystyle 4(r\cos(\theta))(r\sin(\theta))=1\)

Using (1) and (2), we have:

\(\displaystyle 4xy=1\)

B. \(\displaystyle 2r^2\cos(2\theta)=1\)

I would use the double-angle identity for cosine \(\displaystyle \cos(2\alpha)=\cos^2(\alpha)-\sin^2(\alpha)\) to rewrite the equation as:

\(\displaystyle 2r^2\left(\cos^2(\theta)-\sin^2(\theta) \right)=1\)

Distribute $r^2$:

\(\displaystyle 2\left(r^2\cos^2(\theta)-r^2\sin^2(\theta) \right)=1\)

\(\displaystyle 2\left((r\cos(\theta))^2-(r\sin(\theta))^2 \right)=1\)

Using (1) and (2), we have:

\(\displaystyle 2\left(x^2-y^2 \right)=1\)

C. \(\displaystyle 4r^2\sin(2\theta)=1\)

Referring to part A, we see this will be:

\(\displaystyle 8xy=1\)

D. \(\displaystyle 4r^2\cos(2\theta)=1\)

Referring to part B, we see this will be:

\(\displaystyle 4\left(x^2-y^2 \right)=1\)

3.) The letters $x$ and $y$ represent rectangular coordinates. Write the given equation using polar coordinates $(r,\theta)$.

I am going to make assumptions regarding parts A and C based on experience with giving online help and the lack of bracketing symbols that seems to be prevalent.

A. \(\displaystyle r=\frac{5}{\cos(\theta)+\sin(\theta)}\)

Multiplying through by \(\displaystyle \cos(\theta)+\sin(\theta)\) we obtain:

\(\displaystyle r\cos(\theta)+r\sin(\theta)=5\)

Using (1) and (2), we have:

\(\displaystyle x+y=5\)

B. \(\displaystyle r=5\)

Since \(\displaystyle 0<r\) we may square both sides to get:

\(\displaystyle r^2=5^2\)

Using (4), this becomes:

\(\displaystyle x^2+y^2=5^2\)

Since $r=5$ is the locus of all points whose distance is 5 units from the origin, this result should easily follow.

C. \(\displaystyle r^2=\frac{5}{\cos(\theta)+\sin(\theta)}\)

Multiplying through by \(\displaystyle \cos(\theta)+\sin(\theta)\) we obtain:

\(\displaystyle r\left(r\cos(\theta)+r\sin(\theta) \right)=5\)

Using (1), (2), and (4) there results:

\(\displaystyle \sqrt{x^2+y^2}(x+y)=5\)

D. \(\displaystyle r^2=5\)

Using (4), this becomes:

\(\displaystyle x^2+y^2=5\)

4.) The letters $r$ and $\theta$ represent polar coordinates. Write the given equation using the rectangular coordinates $(x,y)$.

A. \(\displaystyle r=8\)

Square both sides:

\(\displaystyle r^2=8^2\)

Using (4), we have:

\(\displaystyle x^2+y^2=8^2\)

B. \(\displaystyle 0=?\)

I don't know how to interpret this.